ALICE:技術入門 | 深入理解零知識證明算法之Zk-stark：Low Degree Testing_區塊鏈專業怎么樣

前言

本系列的第二篇文章，以超市收據為例，描述了Arithmetization的具體過程。本文將以另外一個例子為基礎，在回顧Arithmetization過程的同時，將內容引申到多項式的LDT過程。

新的實例

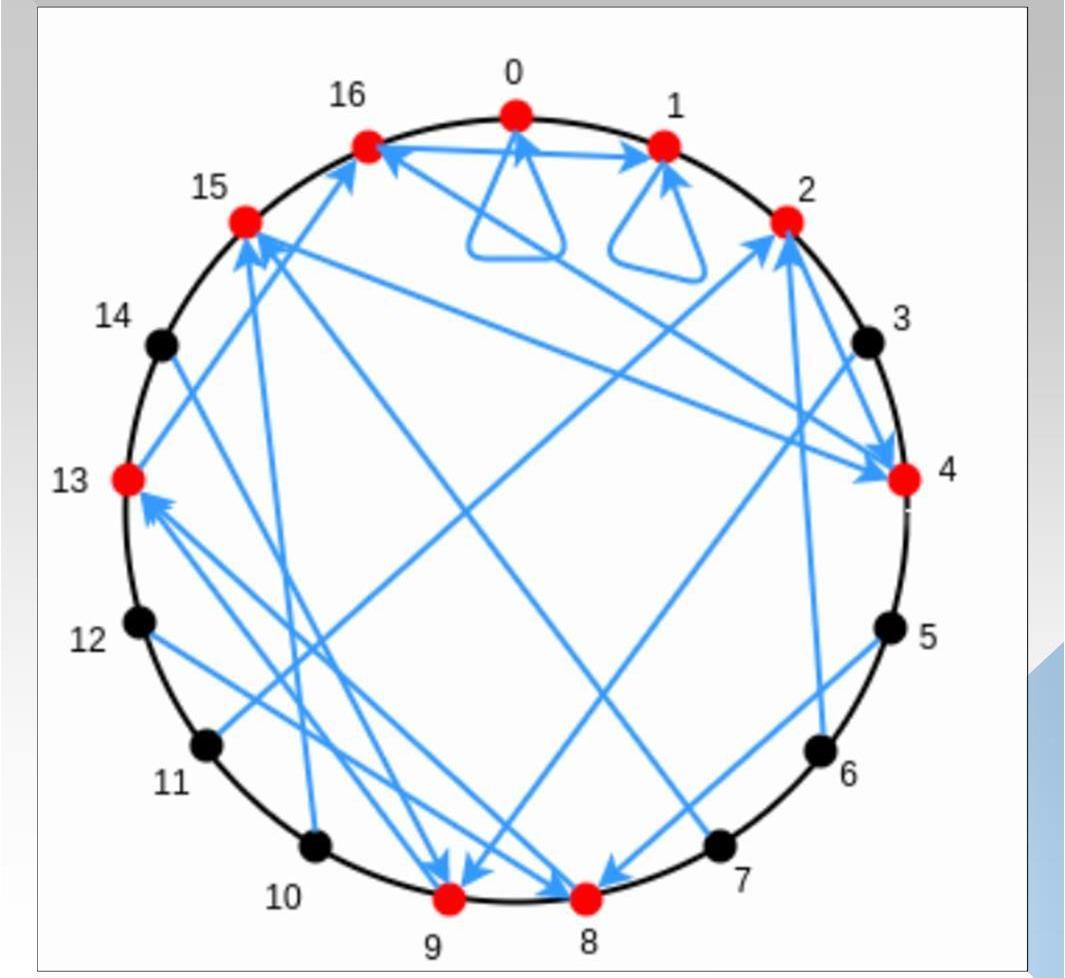
AliceClaim：“我有1000,000個數，他們都在范圍內”。為了方便驗證者Bob驗證，Alice首先要對Claim進行Arithmetization轉換。過程如下圖1所示(圖中：黑色箭頭代表主流程，紅色箭頭代表附加說明信息，黃色圈對應下面詳細說明的索引)

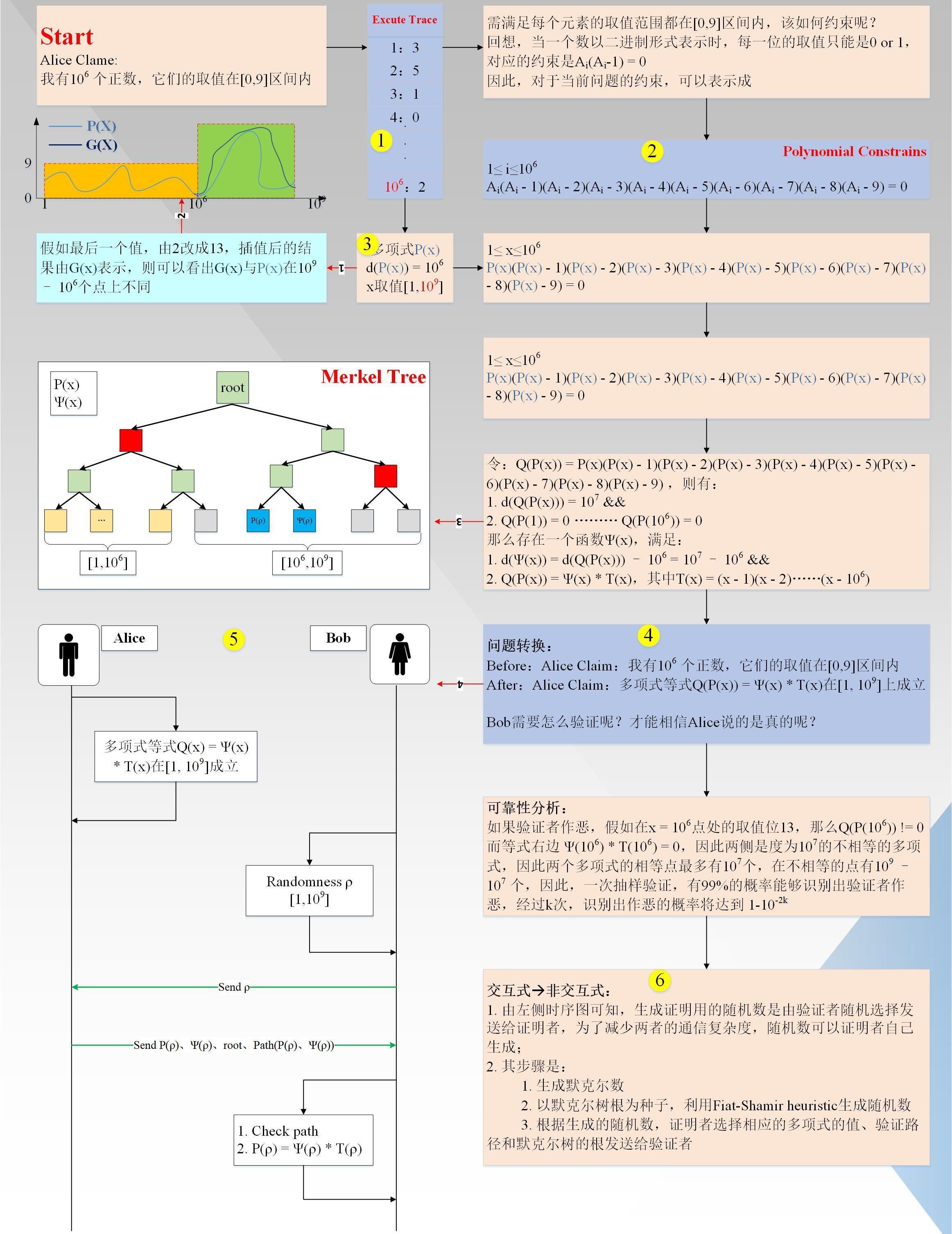
下面具體說明一下對應流程：

首先生成執行軌跡(EXCUTETRACE)，事實上，它是一張表，總共有1000,000行；

生成多項式約束(PolynomialConstrains)，多項式約束滿足執行軌跡的每一行(個人理解：步驟1，2沒有一定的先后依賴關系，只是習慣上先生成執行軌跡，再生成約束多項式)；

對執行軌跡進行插值，得到一個度小于1000,000的多項式P(x)、x取值，并計算更多點上的值，x取值范圍擴大到(Reed-Solomen系統編碼)；假如，證明者有一個值不在范圍內(圖中紅線1/2所示)，假如就是第1000,000個點，它實際的值是13，大于9，其插值后的曲線G(x)如圖所示，圖中P(x)為有效曲線，G(x)為無效曲線。可以看出，兩條曲線在變量x取值范圍內，最多有1000,000個交點，即有1000,000,000-1000,000個點不同，這很重要。

將插值后的多項式P(x)和多項式約束進行組合變換，最終得到的形式為：

證監會主席易會滿：區塊鏈等新一代信息技術和金融創新發展迅猛:金色財經報道，證監會網站9月6日發布“深化資本市場開放合作 促進后疫情時代全球經濟復蘇發展——易會滿主席在第60屆WFE年會開幕式上的致辭”，易會滿主席指出，近年來，隨著人工智能、大數據、區塊鏈等新一代信息技術和金融創新的迅猛發展，再疊加疫情沖擊，資本市場的運行模式和行業生態正在發生深刻變化，交易所發展所處的外部環境更趨復雜，新情況新問題不斷涌現，風險隱患增多。[2021/9/6 23:04:18]

Q(P(x))=Ψ(x)*T(x)，其中T(x)=(x-1)(x-2)……(x-1000,000)，x取值

其中，d(Q(P(x)))=10,000,000、d(Ψ(x))=10,000,000-1000,000、d(T(x))=1000,000；

至此，問題就轉化成了，Alice宣稱“多項式等式在變量x取值范圍內成立”的問題。那么驗證者Bob該如何驗證呢？具體過程如下：

證明者Alice在本地計算多項式P(x)、Ψ(x)在所有點上的取值，對！從1至1000,000,000，并形成一個默克爾樹；

驗證者Bob隨機的從內選取一個值ρ，并發送給證明者Alice，要求其返回對應的信息；

證明者Alice返回P(ρ)、Ψ(ρ)、root、AuthorizedPath(P(ρ)、Ψ(ρ))給驗證者Bob；

驗證者Bob首先根據默克爾樹驗證路徑驗證值P(ρ)、Ψ(ρ)的有效性，然后等式Q(P(ρ))=Ψ(ρ)*T(ρ)，如果成立，則驗證通過；

完整性分析：如果驗證者Alice是誠實的，那么等式Q(P(x))一定會被目標多項式T(x)整除，因此必定存在一個d(Ψ(x))=d(Q(P(x)))-d(T(x))的多項式Ψ(x)，滿足Q(P(x))=Ψ(x)*T(x)，因此對于任意的x，取值在之間，等式都會成立；

動態 | 新華社：在“上碼”“上云”“上鏈”等多重技術托舉下，新經濟新業態不斷涌現:12月9日，新華社發表題為《金融“活水”唱出歡快的歌——金融創新穩步推進強健實體經濟血脈》文章，記者了解到，隨著大數據、云計算和區塊鏈技術加速迭代，在“上碼”“上云”“上鏈”等多重技術托舉下，金融“活水”奔流，眾多雙創企業走上發展快車道，新經濟新業態不斷涌現。

過去，不少小微企業即便有應收賬款等資產，仍會出現現金流周轉困難。如今，銀行憑借區塊鏈記賬和不可篡改技術，可對銷售回款進行管理與大數據風控，為供應鏈上下游企業提供融資、結算、資金管理等一攬子綜合金融服務。

浙商銀行探索的“區塊鏈+醫藥行業”應用，與瑞康醫藥內部系統實現互聯互通，并搭建平臺將上游藥廠、下游醫院和藥店、醫藥倉儲物流企業以及各金融機構、信息服務商等統一納入。（新華社）[2019/12/9]

可靠性分析：如果驗證者Alice是不誠實的，即類似于步驟3里的假設，在x=1000,000上，P(x)的取值為13，那么Q(P(1000,000))!=0，但是等式右邊，T(1000,000)=0，因此Q(P(x))!=Ψ(x)*T(x)，即等式兩邊是不相等的多項式，其交點最多有10,000,000個，因此通過一次隨機選取，其驗證通過的概率僅為10,000,000/1000,000,000=1/100=0.01，經過k次驗證，其驗證通過的概率僅是1-10(^-2k)；

上述的驗證過程為交互式的，如果是非交互式的，可以利用Fiat-Shamirheuristic進行變換，以默克爾樹的根作為隨機源，生成要查詢的隨機點；

LDT

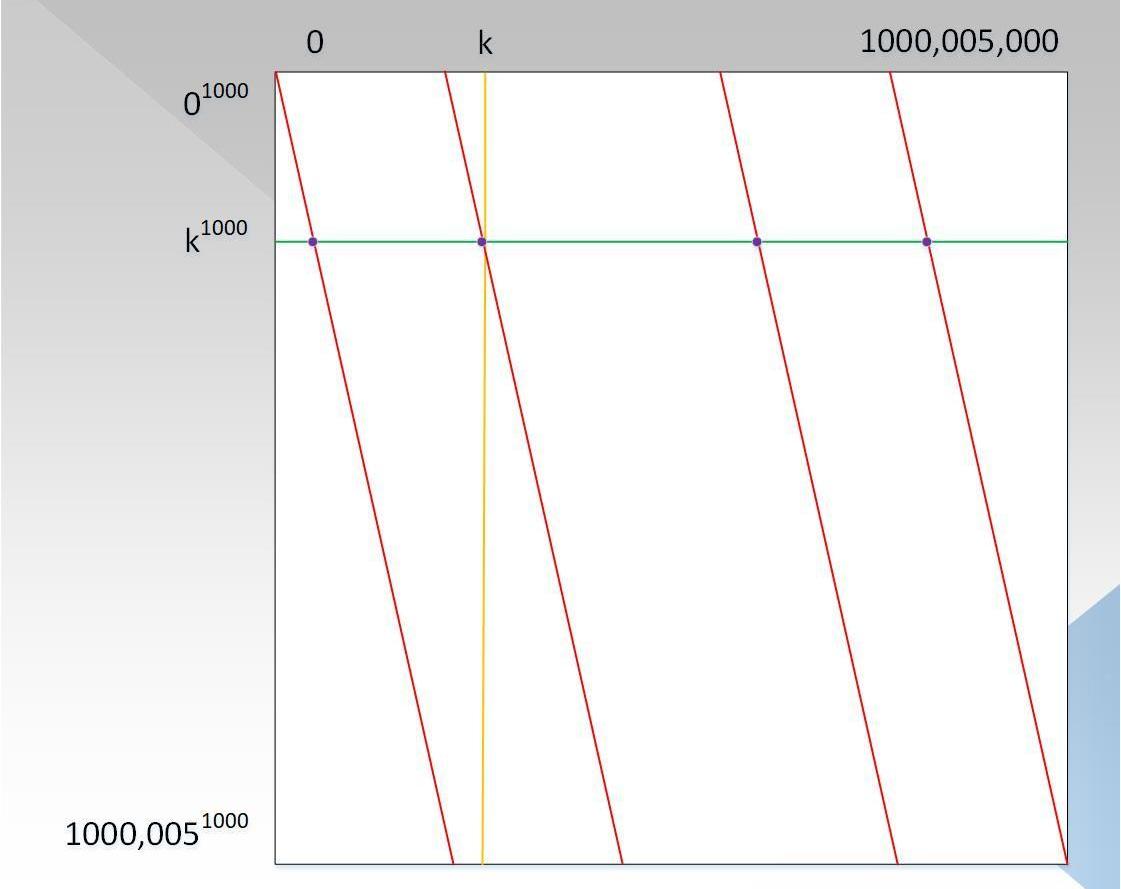
我們忽略了一種攻擊方式，即針對每一個數x，證明者都隨機生成p，然后根據Ψ(x)=Q(p)/T(x)，這些點不在任何一個度小于1000,000的多項式上，但是可以通過驗證者驗證。如下圖2所示：

聲音 | 英國議員Margot James：英國政府在探索區塊鏈技術的使用:據Blokt報道，近日在倫敦區塊鏈峰會上，英國議員、英國數字和創意產業部長Margot James在題為“利用區塊鏈的變革力量”的主旨演講中介紹了英國公共部門采用區塊鏈技術的一些最新優秀案例。英國長期以來一直歡迎區塊鏈領域的創新，一些區塊鏈行業最有希望的公司選擇了倫敦。Margot James還簡要談到了Facebook的Libra，強調了一家倫敦開發公司據稱在該部署中發揮的作用。 他還分享了英國政府2000萬英鎊創新基金GovTech的細節，該基金旨在激勵英國科技公司為公共部門問題提出新的解決方案。他評論稱，該基金也適用于通過分布式分類賬技術提供創新的區塊鏈公司。然而，他注意到，英國政府只是在探索區塊鏈技術的使用，而不是加密貨幣，許多政府和監管機構仍然非常謹慎地看待加密貨幣。[2019/7/3]

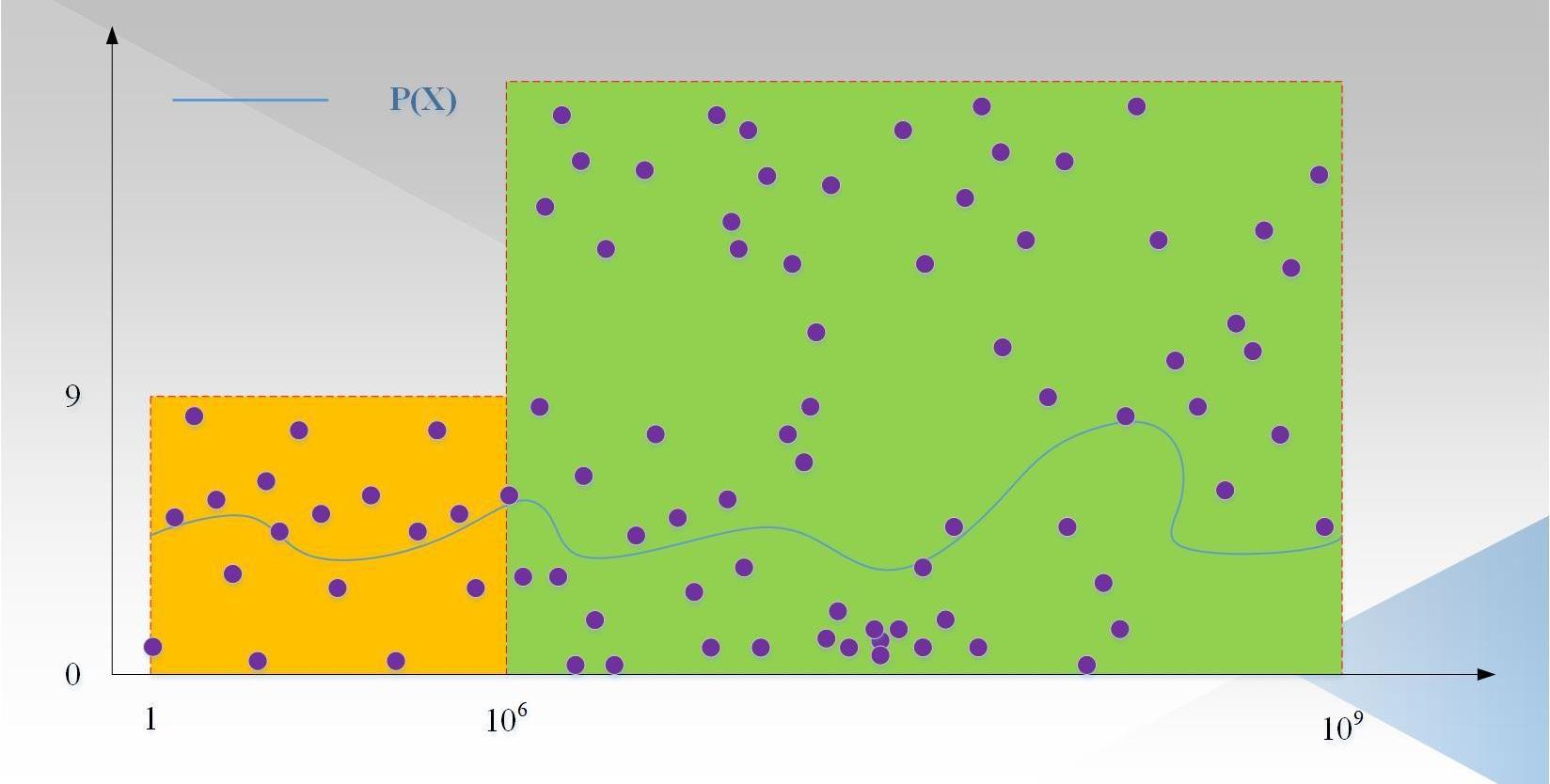
圖中：紫色的點為隨機生成的點p，這些點大概率不在一個度小于1000,000的多項式上(事實上，可以不考慮前1000,000個點，因為驗證者只會從范圍內取值)。因為即使選擇1000,000個點插值出一個度小于1000,000的多項式，也不能保證其他的點在這個多項式上，因為其他的點是隨機生成的。因此，需要有一種方式，保證證明者P(x)的度是小于1000,000，Ψ(x)的度小于10,000,000-1000,000。這就是LDT的目標，那LDT具體的過程是怎么樣的呢？請繼續往下看。

舉個栗子，如果Alice想證明多項式f(x)的度是小于3的，即有可能是2次的或者是1次的。一般流程如下：

驗證者Bob隨機選取三個值a,b,c，發送給證明者Alice；

聲音 | 聯合國副秘書長蓋圖：區塊鏈等技術將給“一帶一路”建設帶來顯著效益:據人民日報消息，聯合國副秘書長蓋圖表示，在“一帶一路”建設過程中，應當重視與第四次工業革命相伴而來的機遇和挑戰，在創新中謀發展。人工智能、自動化、區塊鏈技術等都將產生顯著的效益，但也會沖擊就業機會，加劇不平等，這就需要“一帶一路”建設的國際合作伙伴們轉變發展動力，克服新技術可能帶來的弊端。[2019/2/13]

證明者Alice返回f(a),f(b),f(c)；

驗證者Bob插值出度小于3的多項式g(x)，然后再隨機選取一個點d，發送給證明者；

證明者Alice返回f(d)；

驗證者Bob比對f(d)和g(d)的值，如果相等，則證明成立。

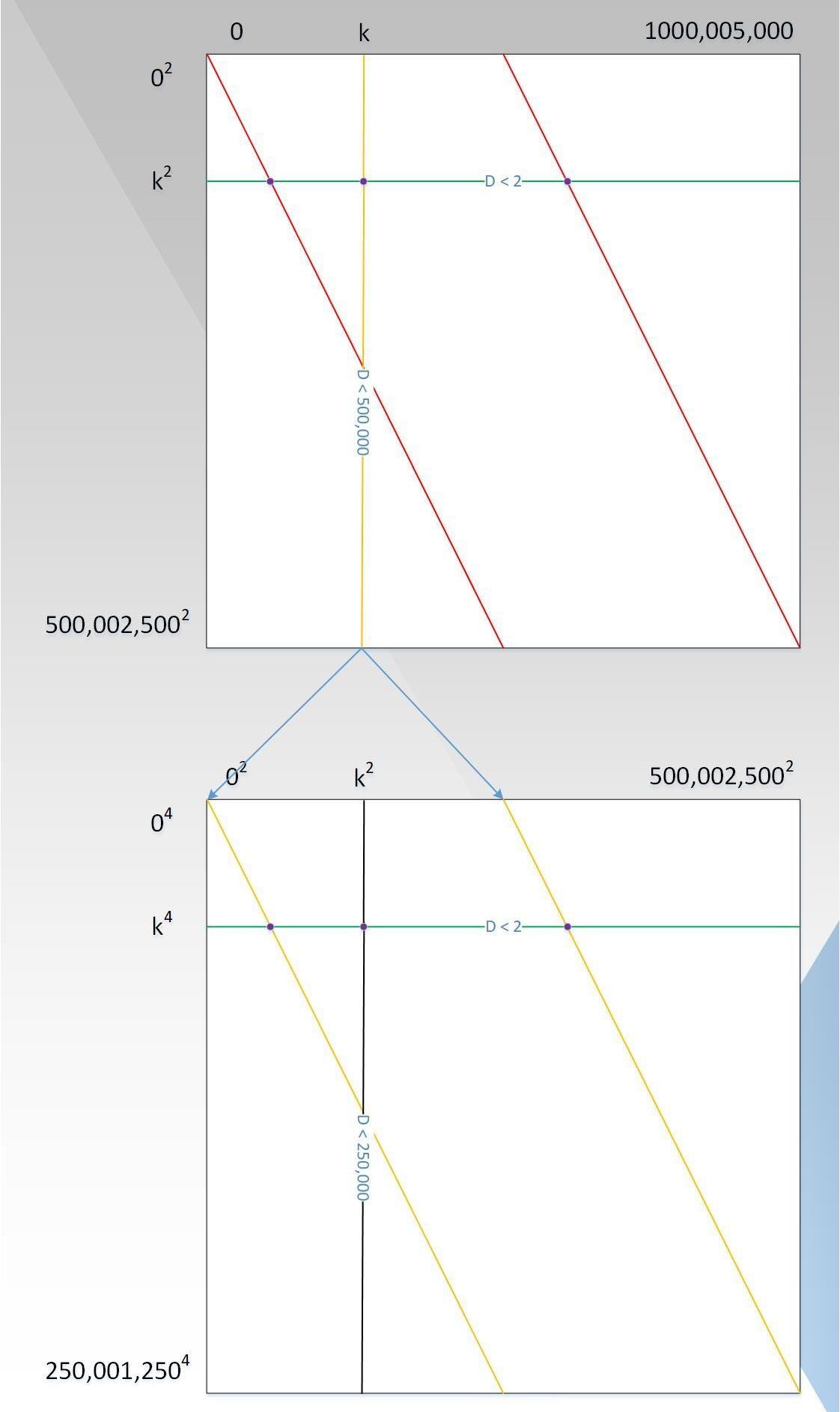
回歸到一般情況，其過程可以用下圖3表示：

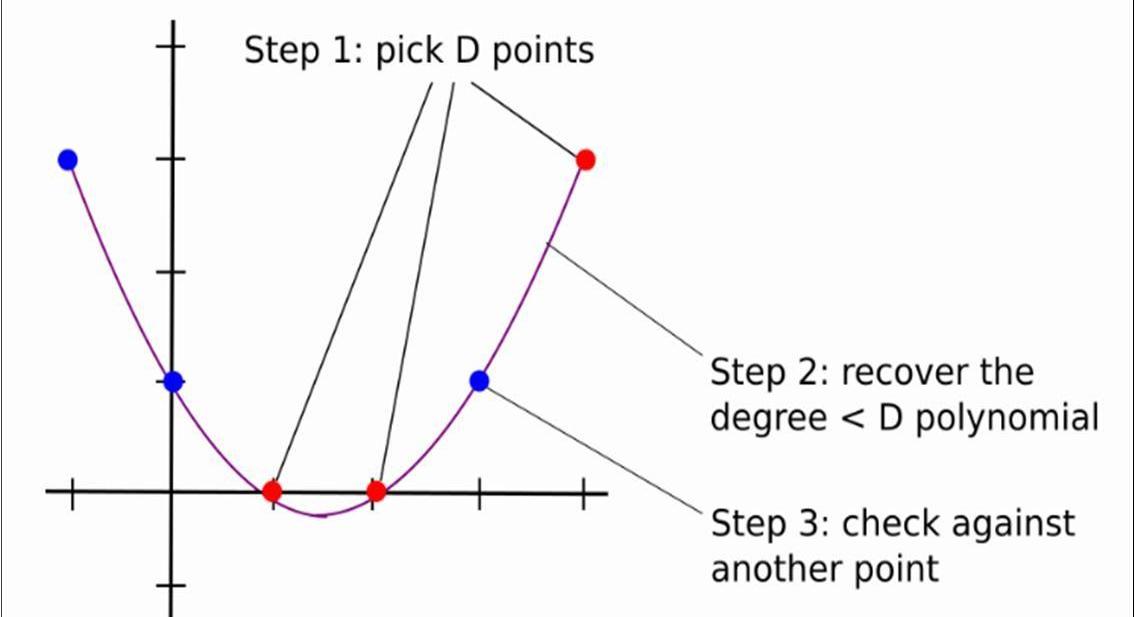
可以看出，如果D很大，Alice和Bob交互的次數則為D+k次，復雜度很高；有沒有一種辦法，使得兩者之間交互的次數小于D的情況下，使得驗證者相信多項式的度是小于D的，直接返回小于D個點肯定是不行的，因為那不能唯一確定一個度小于D的多項式，因此需要證明者需要額外發送一些輔助信息。下面我們以P(x)為例，詳細闡述這個過程(事實上，應該是證明P(x)和Ψ(x)的線性組合小于10,000,000-1000,000，本文重點是LDT，因此只以P(x)為例，這并不影響對LDT的理解)。

假如P(x)=x+x^999+x^1001+x^999999=x+x^999+x*x^1000+x^999*(x^1000)^999;

此時，我們找到一個二維多項式G(x,y)，取值范圍分別是、，滿足：

聲音 | 投資人David Johnston：區塊鏈最大的障礙除了監管還來自于技術:據PANews消息，近日BitAngels區塊鏈天使投資機構執行董事David Johnston在接受專訪時表示，加密貨幣短期市場受到各種因素影響會有漲有跌波動很大，但是長期市場價格卻由項目的內在價值所決定。并表示自己是不做任何短線操作的。Johnston還認為區塊鏈最大的障礙除了監管還來自于技術，“如果我想讓我們的區塊鏈技術被全球的人使用，可能每天需要80億筆交易，但目前的支持能力遠達不到。這就需要很多優秀的技術人員一起來探索區塊鏈的擴展能力和處理能力。[2019/1/15]

G(x,y)=x+x^999+x*y+x^999*y^999可以發現，當y=x^1000時，滿足：

G(x,y)=G(x,x^1000)=x+x^999+x*x^1000+x999*(x^1000)^999=P(x)

如果我們能證明G(x,y)相對的x,y的最高度都是小于1000，因為P(x)=G(x,x^1000)上，因此可以相信P(x)的度小于1000,000；如圖4所示：

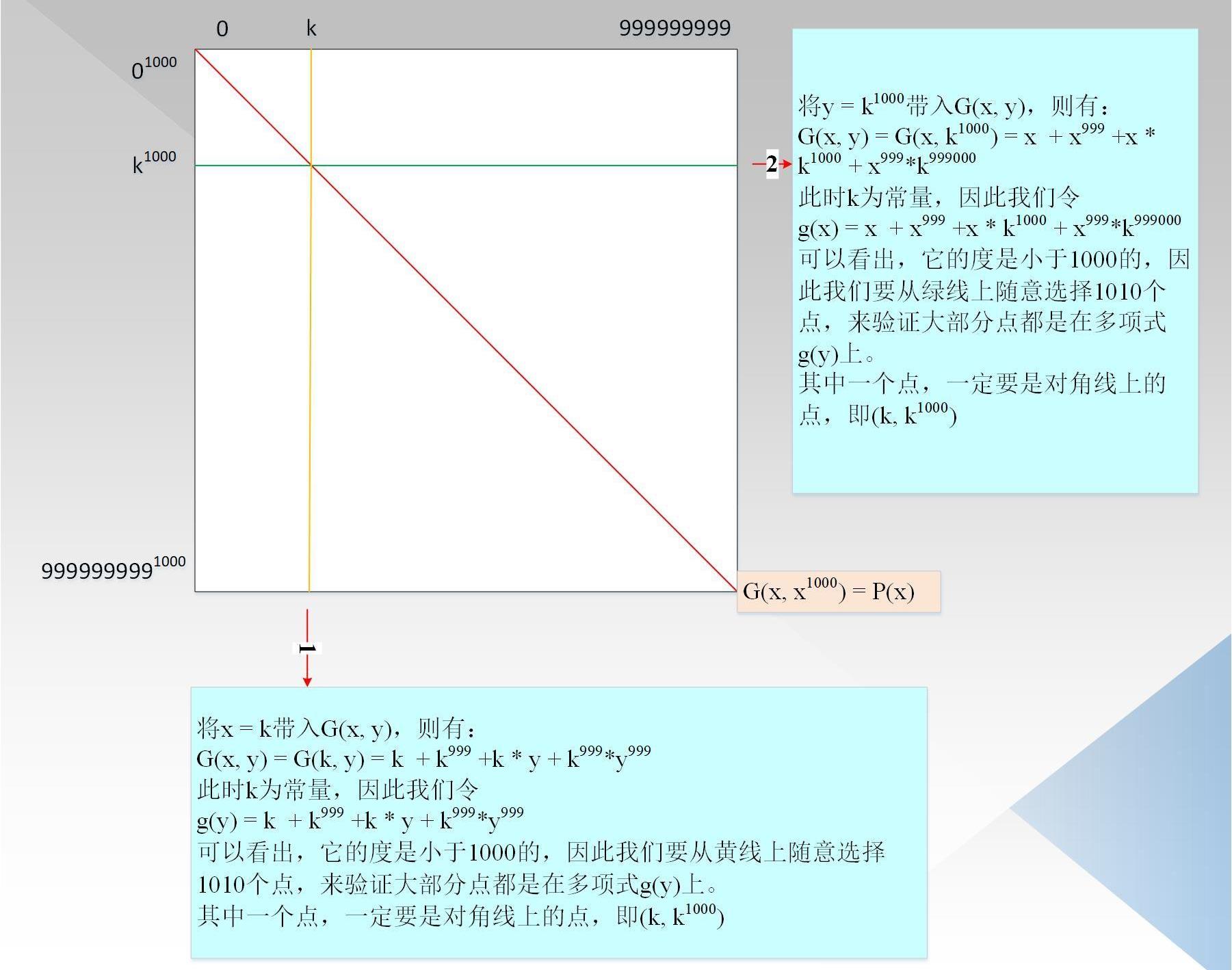
驗證者把所有的點都計算好，形成一顆默克爾樹。驗證者隨機選擇一行和一列，如圖中紅線1/2所示，對于每一列，它是由關于y的度小于1000的多項式生成，對于每一行，它是由關于x的度小于1000的多項式生成。驗證者從行/列中隨機選擇1010個點，用來驗證對應行/列上的點是否在度小于1000的多項式上，需要注意的是，因為P(x)的點都在上圖的對角線上，因此我們要確保每一行/列對應的對角線上的點也在對應的度小于1000的多項式上，即1010個里面一定要包含對角線的點。

可靠性分析：如果原始多項式的度實際上是小于10^6+10999，即P(x)=x+x^999+x^1001+x^1010999，那么對應的G(x,y)為G(x,y)=x+x^999+x*y+x^999*y^1010，即，對于每一個x，G(x,y)是關于y的一元多項式函數，且度d<1010，因此下圖中的每一列所有點都是在度d<1010的多項式上，而不在d<1000的多項式式上。所以如果證明者任然宣稱多項式P(x)的度d<1000,000，則會驗證失敗，其他場景是同樣的道理

那有沒有可能惡意證明者仍以G(x,y)=x+x^999+x*y+x^999*y^999的形式去生成證據呢？這樣會驗證通過嗎？

我們知道，我們在驗證時著重強調了對角線上的那一點一定要在多項式上，我們知道，此時對角線對應的多項式形式是

P(x)=x+x^999+x1001+x^999999，而實際的P(x)，我們在這里標記為P`(x)，其形式是：

P`(x)=x+x^999+x^1001+x^1010999

因此，如果驗證者恰好選擇的點是兩個多項式的交點，則會驗證通過，事實上，兩個多項式最多有1000,000左右個交點，但是由于隨機選取的點不是證明者自己選取，是由默克爾樹的根為種子隨機生成，因此證明者沒有機會作惡，去可以選取那些能通過驗證的點。

由于總共由10^9個點，因此隨機選取一個點，能驗證成功的概率為10^6/10^9=10^(-3)，如果選擇k行，則成功的概率僅為10^(-3k)。

以上可以看出，驗證者和證明者只需要交互1010*2*k個點，就可以完成驗證，假如k=10，則1010*2*10=20100<<10^6。

雖然上述實現了在交互次數小于D的情況下，完整LDT驗證，但是證明者的復雜度過于龐大，至少10^18的復雜度遠遠大于原始的計算，因此需要一些優化方案，降低復雜度。話不多說，直接引入有限域，畢竟在實際項目中，我們可不希望數值本身過于龐大。直接引用費馬小定理的結論：在有限域p內，如果滿足(p-1)能被k整除，則映射x=>x^k的像只有(p-1)/k+1個。下圖5以p=17，映射x=>x^2為例：

圖中，紅色為x^2在有限域p內的象，總共由(p-1)/2+1=9個。同時我們可以發現，9^2和8^2的像一致，10^2和7^2的像一致，以此類推，16^2和1^2的像一致，記住這個現象，對下一張圖的理解有幫助。

因此，在本例中，我們選擇一個素數p=1000,005,001，其滿足：

為素數

p-1能被1000整除

p要大于10^9

因此，在有限域p內，x=>x^1000的像在p內有(p-1)/1000=1000,005個，因此圖4可以變成圖6的形式：

可以看出，列坐標變成了10^6個元素，對角線變成了平行的線條，總共有1000個。還記得上面費馬小定理結論的特殊現象嗎？這就是對角線這種分布的原因，讀者試著去理解(可能讀者會覺得，對角線應該是鋸齒形，不是這種平行的形式，也許你是對的，但是這并不影響驗證流程)。此時證明者的復雜度已經從10^18減少到了10^15次方，證明和驗證過程和步驟3描述的仍然一致。

還能不能繼續優化呢？答案是肯定的。回想起前面所述的驗證過程，對于每一行/列，驗證者都要獲取1000個點進行插值得出一個度小于1000的多項式，仔細觀察圖6，對于每一行，原始數據里不就是有1000個數么？那我們干脆選這些點插值出一個度小于1000的多項式，然后只需要隨機讓證明者再計算任何一列，并且證明沿著列上的點都在度小于1000的多項式上，并且列上的點也在對應的利用原始數據插值出的行多項式上。此時，證明者復雜度從10^15減少到了10^9次方。

總結：個人理解，從步驟1到步驟5，其實是PCP到IOP的選擇過程。

PCP要求證明者生成全部的證據，然后驗證者多次隨機選取其中的某一部分進行驗證，但是這樣，證明者的復雜度仍然很高；

IOP要求證明者不用生成全部的證據，根據多次的交互，每次生成只需生成部分證據，使得證明的復雜度和D呈近似線性關系；

證明者復雜度已經降低到了與D呈擬線性關系，驗證者的復雜度雖然是亞線性，交互次數已經低于D，但是能不能優化到更低呢？基于證明復雜度的最優設置，我們繼續探索驗證復雜度的優化之路，回顧P(x)=x+x^999+x^1001+x^999999=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999，令G(x,y)=x+x*y^499+x*y^500+x*y^499999，則當y=x^2時，有G(x,y)=G(x,x^2)=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999=P(x)。最終的圖應如下圖7所示：

從圖中可知：

證明則復雜度仍為10^9次方；

每一行上的點都在度d<2的多項式上，因為當y取固定值時，G(x,y)就是關于x的一次多項式；

每一列上的點都在度d<D/2的多項式上，證明者需要證明這個多項式是小于D/2的，假定這個多項式為P1(x)，這個時候，并非驗證者選取大于D/2個點去驗證，因為驗證復雜度仍然不夠低，而是對這一列再一次用到類似于P(x)的處理過程，如圖7中下面的圖所示，以此循環，直到可以直接判斷列上的多項式的度為止，類似于行。

總結

至此，本篇文章就結束了，總結下來，本文主要闡述了以下幾個內容：

如何轉換問題形式--Arithmetization

為何需要LDT--為了驗證簡潔

LDT的大概過程--二分法驗證，類似于FFT

降低LDT的復雜度--有限域+IOP

至于LDT的詳細過程，將留給本系列的最后一篇，敬請關注。

謝謝大家，歡迎批評指正，有任何問題或者疑問可以留言。

Tags：區塊鏈ICEALICEALI區塊鏈專業怎么樣alice幣發行量alice幣還有長期價值嗎alien幣怎么樣

酷幣下載