Curve:深度解析：自動做市商（AMM）算法的數學原理及其未來發展_SWAP

作者：LeoLiu,GuangwuXie

翻譯：VanessaCao

校對：LeoLiu,GuangwuXie

排版：JaneHu

感謝：FangyuanZhao,ShowenPeng,DW,LianxuanLi,DaveWhite,DanRobinson,VanessaCao,JaneHu

本文由星際密探和DachaleResearch戰略合作伙伴BTXCapital獨家授權星際密探發布，在本文中，我們將首先回顧由Bancor、Uniswap、Balancer和Curve協議實現的四種自動做市商(AMM)算法。還將討論AMM算法的最新發展、可能的改進和未來。

由于本論文過長，本文總共分為上、中、下篇闡述自動做市商算法、現狀及未來迭代的思考。。

上篇目錄

BancorNetwork的聯合曲線概念和交易公式Uniswap的無常損失計算?當價格變動在2ρ之間時的正向收益流動性分布、流動性注入、UniswapV3范圍訂單Balancer的做市函數和交易公式智能訂單路由算法......BancorNetwork的聯合曲線概念和交易公式:

Bancor1利用聯合曲線的概念來確定價格。聯合曲線是代幣價格與其總供應量之間的關系。

Bancor1

BancorProtocolContinuousLiquidityforCryptographicTokensthroughtheirSmartContracts

https://storage.googleapis.com/website-bancor/2018/04/01ba8253-bancor_protocol_whitepaper_en.pdf

聯合曲線BondingCurve：

聯合曲線模型可以理解為描述“代幣買賣價格”與“代幣發行總量”之間的函數關系，可以由智能合約以去中心化的方式自動執行。

https://medium.com/linum-labs/intro-to-bonding-curves-and-shapes-bf326bc4e11a

BancorNetwork選擇的不變量是F，稱為連接權重。在第一個表達式中R是指流動性池中的儲備代幣數量，S是流動性池外的BNT總供應量，P是BNT和儲備代幣的相對價格。我們可以代入P的方程，對兩邊積分2得到P和S之間的關系。這是一個指數表達式，其中指數α與連接權重F有關。F越小，α越大，這意味著價格相對于BNT的總供應量變化得更快。

兩邊積分2

FormulasforBancorsystem

https://drive.google.com/file/d/0B3HPNP-GDn7aRkVaV3dkVl9NS2M/view?resourcekey=0-mbIgrdd0B9H8dPNRaeB_TA

使用這個表達式和簡單的積分，我們可以導出T和E之間的關系，其中R0，S0是R和S的當前值。

如果我們想在代幣A和代幣B之間交換，則將代幣A出售給代幣B。我們首先需要使用代幣A從池A購買BNT代幣。接下來，我們需要使用BNT從池B購買代幣B。下面是計算我們將收到多少代幣所需的精確公式。代幣A和代幣B之間的相對價格可以用BNT代幣和代幣A/B之間的相對價格表示。

優點：Bancor允許在某些池中進行單邊流動性的注入，這由Bancor治理決定。可以存入多少單邊流動性是有限制的，這也是由Bancor治理決定的。在限額內，當用戶以其他代幣的形式存入單邊流動性時，Bancor將補充等值的BNT代幣。這使得用戶提供的有效流動性加倍。如果達到限額，如果人們想要存單邊流動性，就得等有人提取單邊流動性，或者有人把BNT做為單邊流動性注入。

Bancor協議以BNT部分賺取的手續費補償用戶在存入單邊流動性時的無常損失。如果交易費用不能完全補償無常損失，Bancor將鑄造BNT以確保無常損失為零。因此，流動性提供者如果將流動性存入一定的時間，就可以享受穩定的收入。

缺點：如上所述，所有交易都需要BNT代幣作為中介。因此，我們將經歷兩次滑點。由于相同的原因，所有流動性池都由BNT和另一個代幣組成，因此缺乏多樣性。BNT代幣價格也可能受到影響，因為需要彈性供應才能實現無常損失補償和單邊流動性存款。

Bancor引入了連接代幣BNT的概念，它連接到所有具有不同連接權重的代幣，對應不同決定價格的聯合曲線。

Uniswap的無常損失計算:

Uniswap使用恒定乘積做市商(CPMM)來決定價格。在我們深入研究UniswapV2和V3使用的算法之前，讓我們先了解什么是無常損失(IL)以及如何計算它。

恒定乘積做市商(CPMM)

ConstantProductMarketMaker

強制要求兩種資產儲備量的乘積必須始終保持不變x*y=k

https://ethresear.ch/t/improving-front-running-resistance-of-x-y-k-market-makers/1281

無常損失

ImpermanentLoss

是指資金在流動性池中面臨的損失。

https://finematics.com/impermanent-loss-explained/

吉林高院：探索區塊鏈技術與執行工作深度融合 破解執行難題:11月22日消息，為有效推進“切實解決執行難”工作，吉林省高級人民法院積極探索區塊鏈技術在法院執行環節的應用場景，將區塊鏈技術作為智慧法院建設新的著力點。繼“智能審執銜接”“生道執行”“電子封條”等區塊鏈場景先后應用，2021年吉林高院在“區塊鏈+執行”創新業務應用場景方面持續發力，易執行-線索智能分析平臺于3月份應運而生，并完成集中試點和上線應用，助力“切實解決執行難”提效增速。（北方法制報）[2021/11/22 7:04:45]

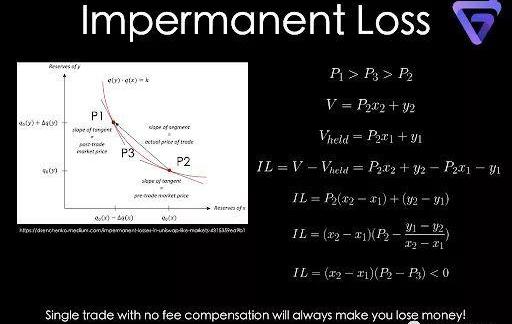
如果AMM函數是凸的，那么沒有交易費用補償的單筆交易總是會導致流動性提供者賠錢。假設一筆交易導致AMM函數從點1移動到點2。點1和點2的現貨價格是P1和P2。P3為實際交易價格。由于凸函數的性質，P1>P3>P2。無常損失定義為交易后池中流動性提供者代幣的當前價值與流動性提供者的代幣當前價值之間的差值，如果他只是持有他的代幣而不將它們用于流動性提供，則表示為V和Vheld。為方便起見，無常損失和價格將以代幣Y表示。經過一些簡單的推導，很容易證明無常損失總是小于零。

Uniswap3V2使用一個簡單但功能強大的公式來確定交易。池代幣儲備數量的乘積是一個常數。與Bancor相比，它擺脫了連接代幣的依賴。交易完全由流動性池中的代幣數量決定。

Uniswap3

UniswapV2Core

https://uniswap.org/whitepaper.pdf

由于此函數的性質，池中兩個代幣的價值將始終相同。

使用相同的邏輯，不難計算UniswapV2中單筆無手續費的無常損失。假設交易將價格從P更改為Pk。以百分比衡量的無常損失可以單獨表示為k的函數。

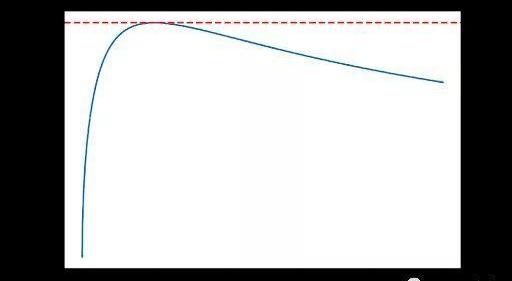
毫不奇怪，這個函數總是小于或等于零，正如我們從上面沒有費用的無常損失圖中可以看出的。如果在對數空間中繪制橫軸，則IL(k)將是對稱的。結論是：相對價格變化越大，無常損失就越大。這可以解釋為流動性提供者的更有價值的代幣從池中被買出，留給他們更多價值較低的代幣。

當價格變動在2ρ之間時的正向收益:

接下來，讓我們看看如果我們添加交易費用，IL(k)會如何表現：

導出的無常損失函數IL(k,ρ)看起來與無費用的無常損失函數非常相似。我們可以通過將ρ設置為零來進行合理性驗證，得出相同的結果。典型的UniswapV2費用百分比為ρ=0.3%。在繪制無常損失函數時，我們可以看到在大約k=0.994到1之間有一個高于零的部分。在該地區，無常損失是正的，這意味著流動性提供者實際上獲得了價值。通過引入交易費，當價格在一定范圍內波動時，流動性提供者將獲得正收益。

當價格變動更加波動時，流動性提供者似乎總是會出現虧損。然而，實際情況并非如此。我們知道DaveWhite4等人解決了這個難題。遺憾的是，它超出了這篇介紹性論文的范圍。我們打算在未來進一步研究這個問題。

DaveWhite4

Uniswap’sFinancialAlchemy

https://research.paradigm.xyz/uniswaps-alchemy

至于其他流行的AMM算法的無常損失推導，我們向讀者推薦JiahuaXu?等人的這篇論文。這些推導將是下一次的主題。

JiahuaXu?

SoK:DecentralizedExchanges(DEX)withAutomatedMarketMaker(AMM)protocols

https://arxiv.org/abs/2103.12732

優點：第一個用池中代幣數量的凸函數來確定價格。

缺點：流動性供應均勻分布于所有價格范圍，這意味著資本效率較低。

流動性分布、流動性注入、UniswapV3范圍訂單:

為了提高流動性效用并降低無常損失風險，Uniswap?V3允許用戶僅在特定價格范圍內提供流動性。

Uniswap?

UniswapV3Core

https://uniswap.org/whitepaper-v3.pdf

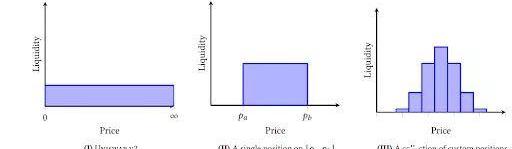
FromUniswapV3whitepaper

這是通過對UniswapV2函數進行平移來實現的：

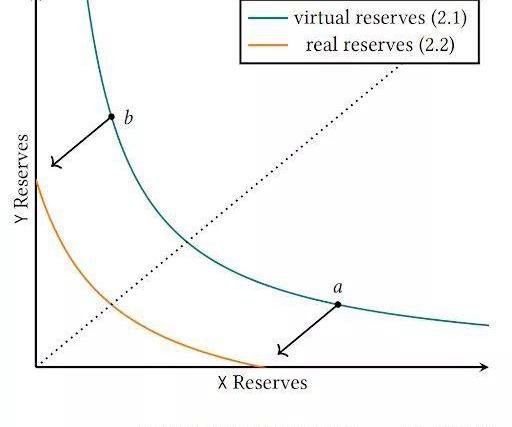
FromUniswapV3whitepaper

將函數向下平移a點的y值，向左平移b點的x值，如上圖和等式所示，確保a和b之間的有效交易結果，就像我們使用綠色曲線作為我們的價格決定函數。當價格超出此范圍時，其中一個代幣儲備將被售罄，從而有效地將流動性集中到此價格范圍內。

DanRobinson?發表了一篇關于計算多個AMM的流動性分布的優秀論文。

全量深度圖：BitMEX在“11400-11800美元”區間訂單密布:AICoin PRO版K線全量深度圖顯示：BitMEX XBT永續合約在“11400-11800美元”區間的訂單密布，總量超過1.28億張。另據主力大單跟蹤顯示，該區間大額委托單也較多，當前一共有9筆，總額超過3800萬美元大額委托買單在掛。請密切留意行情變化。[2020/8/17]

DanRobinson?

UniswapV3:TheUniversalAMM

https://www.paradigm.xyz/2021/06/uniswap-v3-the-universal-amm/

也可以簡單地證明，兩個流動性提供者在同一價格范圍內的流動性可以簡單地加在一起。

在存入流動性時，如上所示，UniswapV3中每個資產的價值不一定相等。只有當P等于Pa和Pb的幾何平均值時，每個資產的價值才相等。當P小于幾何平均值時，資產X的價值大于資產Y的價值。當P大于幾何平均值時，資產X的價值小于資產Y的價值。

當當前價格完全超出流動性提供者設定的價格區間時，UniswapV3將流動性提供者的輸入算作范圍訂單(RangeOrder)，只允許其存入一種代幣。例如，考慮一個由ETH和Dai組成的流動性池。如果設定的價格區間完全高于ETH的當前價格，則只允許用戶存入ETH。如果價格區間完全低于ETH的當前價格，則只允許用戶存入Dai。當價格完全越過流動性提供者設定的價格區間時，他存入的資產將全部轉換為另一種的代幣。由于用戶只能存入一種代幣，范圍訂單只能實現傳統限價訂單中四分之二的訂單。另一方面，買入止損訂單和止損訂單無法實現。截至目前，我們不知道限制范圍訂單代幣類型的目的是什么。

范圍訂單

Range?Orders

本質上并不是真正的訂單，而是LP向資金池某個特定價格點提供的聚合流動性。雖然不是真正的訂單，但「范圍訂單」所表現出的特性，卻很好地模擬了限價單的基本功能。

https://docs.uniswap.org/protocol/concepts/V3-overview/range-orders

優點：UniswapV3引入了流動性分布的概念，允許其用戶在價格范圍內存入流動性。通過集中流動性，提高資本效率。當存入相同價值的資產時，可以獲得更高的流動性和更低的滑點。在某個價格范圍內提供流動性也在某種程度上降低了無常損失的風險。

缺點：用戶在進行范圍訂單時只能存入某些類型的代幣。因此無法實現買入止損訂單和止損訂單。

UniswapV2和V3在其AMM算法中引入了CPMM和流動性分布。提供價格范圍內的流動性本質上使UniswapV3成為一個通用的AMM，能夠通過改變其流動性分布成為任何可能的AMM。

Balancer的做市函數和交易公式:

Balancer?將UniswapV2的雙代幣池擴展到多代幣池。Balancer池中每種資產的價值都持有一個不變的權重，加起來為1。不難證明，這相當于每種資產的儲備數量的冪乘積是一個常數。資產n相對于資產t的價格也可以導出為資產t和n的儲備數量之間的比率，通過它們的權重進行歸一化。

Balancer?

Anon-custodialportfoliomanager,liquidityprovider,andpricesensor

https://balancer.fi/whitepaper.pdf

基于常數不變式，我們可以求導出有不同輸入值的交易公式。在這種記法標準中，資產o始終是買出的資產。資產i是賣出的資產。A和B是打入/接收的代幣和當前的代幣儲備數量。我們還可以根據價格的變化計算打入的代幣或買出的代幣數量。

智能訂單路由算法:

Balancer還引入了智能訂單路由(SOR?)算法。

SOR?

SmartOrderRouterV2

https://docs.balancer.fi/developers/smart-order-router

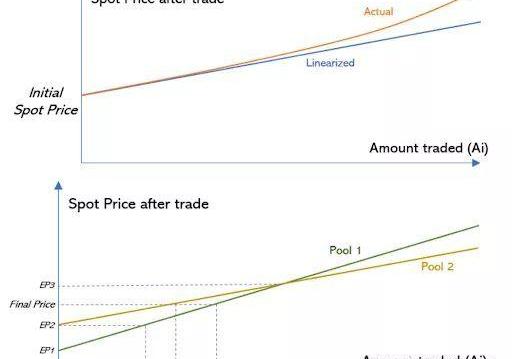
來源：https://docs.balancer.fi/v/v1/smart-contracts/sor/

該算法的總體思路是將一個訂單分成幾個小塊在不同的Balancer池中進行交易，以獲得更好的交易結果。假設我們要在代幣池1和代幣池2進行交易，如果我們要交易的總金額N低于上圖中的A，我們將只在代幣池1進行交易，因為代幣池1的價格總是比代幣池2價格好。如果總金額超過A，我們將部分訂單在代幣池1中交易，部分在代幣池2中交易。在每個代幣池中交易的數量將使每個池中的價格相等。

很容易證明最優策略總是使每個池中的價格相等的策略。

價格函數，相對于交易量，通常是一個非線性函數。Balancer將價格函數簡化為線性函數。如果有n個代幣池，最優策略可以表示為：

如果存在一個價格函數總是大于或小于范圍(0,N)的其余價格函數，則應從上述計算中刪除該價格函數和相應的池，以確保結果有效。如果價格函數總是較小，那么顯然的最佳策略將是在該池中交換所有代幣。

在這個計算中，不用考慮gas費用。實際上，最優策略應該是在路由收益和gas費用損失之間保持平衡。

IOST與滿幣區塊鏈研究院達成深度戰略合作:近日，數字資產與區塊鏈技術研究機構——滿幣區塊鏈研究院與IOST達成深度戰略合作。雙方將圍繞區塊鏈技術創新、品牌共建、政企合作、B端業務布局等方面展開深度合作，共同打造開放共贏的區塊鏈商業場景生態。IOST是全球化的企業級區塊鏈技術應用平臺，致力于將區塊鏈技術應用，推廣至商業端各類行業和客戶端各類應用場景中。滿幣區塊鏈研究院成立于2018年7月，是具有工商資質認證的獨立機構，由CoinBene滿幣公司設立，專注于數字資產與區塊鏈技術研究。[2020/4/3]

SOR算法，我們相信可以在更廣泛的背景下使用。例如，價格函數可以是其他AMM協議池的函數。由于我們目前知識的限制，我們不確定實際的AMM聚合器是否使用相同的邏輯來實現更好的價格。沒有任何價格函數近似的更通用的解決方案將在本文后面討論。

優點：Balancer將2個代幣池推廣到多個代幣池，并引入SOR算法為其用戶實現更好的價格。

缺點：“流動性池的強度取決于其最弱的資產。”一個池中的代幣類型越多，風險就越高。

Balancer是一種多代幣投資組合管理工具，允許靈活的代幣價值分配，具有價格優化算法。

中篇目錄

Curve的StableSwap和交易公式CurveV2的動態權重、可定制的價格錨定和平滑的價格過渡CurveV2在2代幣池中的做市商函數與CPMM和StableSwap相比，CurveV2的價格函數11.價格重錨過程：Xcp標準、EMA價格預言機、相對價格變化步長s

CurveV2的動態交易手續費13.DEX聚合器：BalancerSOR算法的通用解決方案

14.Pivot算法：解決無常損失問題的一種嘗試

單邊流動性解決方案Curve的StableSwap和交易公式：

Curve將恒定加和做市商(CSMM)和恒定乘積做市商(CPMM)合并在一起，以實現更低的價格滑點。我們可以把這個算法看作是向Uniswap/Balancer模型添加一個固定價格部分，使最終的做市函數錨定于一個價格。

Curve1?V1，被稱為StableSwap，設計了用于穩定幣交易的算法。它將CSMM與權重相乘并加上CPMM：

Curve1?V1StableSwap—efficientmechanismforStablecoinliquidityhttps://curve.fi/files/stableswap-paper.pdf

首先我們考慮一個特殊情況，即流動性池中每種代幣的數量是相同的。很容易證明在平衡點處時這個方程成立。但是，當流動性池失衡時，如果χ是一個常數，則該等式將不再成立。因此，我們需要將χ變量化。CurveV1選擇了一種χ的函數形式，使它在流動性池極端不平衡時變為零，這意味著該方程由CPMM主導。在平衡點下，χ等于A。A是一個常數，通過模擬歷史數據進行優化。代入χ_給了我們一個始終成立的方程。

接下來，讓我們推導出StableSwap如何實際計算交易結果。根據當前池中的代幣數量，我們可以計算出_D。例如，如果我們想換出代幣j，我們可以將x?分離開來并求解x?_的方程：

該方程可以簡化為二次形式。可悲的是，現在鏈上Vyper語言里沒有可以解二次方程的數學庫。因此，StableSwap使用了牛頓法來求解_x?。迭代公式每次迭代都將其精度加倍。因此，可以在設定的gas上限內計算可接受的x?。最后，交換前后x?_之間的差值將是購買的代幣j的數量。

牛頓法它是一種在實數域和復數域上近似求解方程的方法https://en.wikipedia.org/wiki/Newton%27s_method

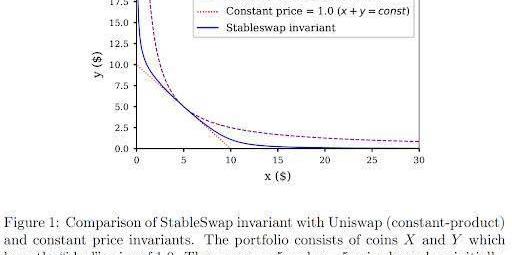
FromStableSwapwhitepaper

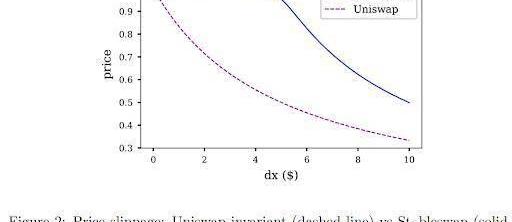
FromStableSwapwhitepaper

與CPMM相比，StableSwap做市商受壓、以x+y=常數方向壓平。這確保交易價格接近或等于1，在平衡點附近有非常小的滑點。當池中的一個代幣幾乎售罄時，價格開始急劇下降。這很容易理解：函數的曲率/滑點被集中/推到別處，以確保在平衡點附近的低滑點。

該模型中的CPMM和動態權重被用于懲罰提前知道消息的大額訂單，防止池中的代幣被完全售罄。

優點：通過添加CSMM和CPMM以及動態權重，Curve的StableSwap實現了非常小的滑點，非常適合穩定幣。

缺點：價格始終錨定在1。如果市場價格與流動性池價格顯著不同，流動性池將被買空。因此，StableSwap僅適用于穩定幣。

CurveV2的動態權重、可定制的價格錨定和平滑的價格過渡：

為了確保更平穩的價格過渡和可定制的價格錨定，Curve11V2將動態權重_χ修改為K_，如下所示：

Curve11V2Automaticmarket-makingwithdynamicpeghttps://curve.fi/files/crypto-pools-paper.pdf

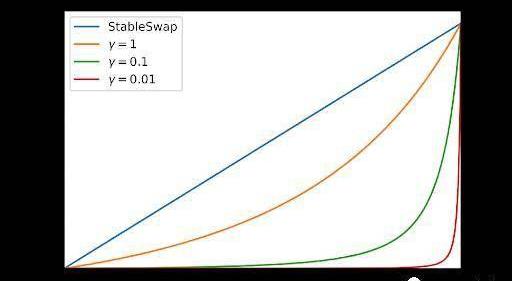
K0_在0和1之間變化，χ和K作為K0_的函數繪制如下：

動態 | 區塊鏈深度融入雄安新區建設發展 區塊鏈在雄安新區已有四大應用:中國雄安官網今日發布文章《動圖解丨看！區塊鏈在雄安“初顯身手”》，目前區塊鏈技術在雄安新趨已有四大應用，分別是：

1、工程項目資金管理，實現工程進度及合同透明管理、資金撥付穿透式管理、多銀行系統直聯等功能；

2、勞務工資實現穿透式發放，實現了建設者工資透明撥付，如果項目參與方未按約定按時發放建設者工資，區塊鏈智能合約會自動觸發代付機制，保障金會自動穿透式撥付至建設者工資卡中，實現建設者無感狀態下的智能支付保障。截至今年10月，區塊鏈資金管理平臺累計已為11萬人次建設者按時發放工資；

3、白洋淀水體污染治理，白洋淀水專項區塊鏈科研資金管理平臺實現項目可研經費的全流程穿透式管理；

4、政務服務創新實踐，各政府部門建立數據調用互信共認機制；區塊鏈非對稱式加密技術、公私鑰機制，確保公眾及政府部門數據資產安全。[2019/11/17]

我們可以從上圖中了解CurveV2如何使價格轉變得平滑。它實際上使動態權重在遠離平衡點時迅速下降。_γ_值越小，下降越快。使動態權重快速下降到零本質上相當于強制函數表現得更像CPMM，即使流動性池只是有一點不平衡。

DW在twitter12上發布了一條很棒的推文，解釋了相同的概念。

DW在Twitter12的推文https://twitter.com/dken_w/status/1422623679150649345價格過渡問題得到了解決。現在我們討論CurveV2如何實現其他不是1的價格錨定。有一個價格錨定意味著在做市曲線上存在一個平衡點，在平衡點處按價格標度縮放的代幣數量相等：

CurveV2在2代幣池中的做市商函數：

縮放后的代幣數滿足與StableSwap類似的等式。以最簡單的2幣流動性池為例，做市商函數可以用A、γ、p、D、x、y表示。該函數可以簡化為關于x,y的三次函數。

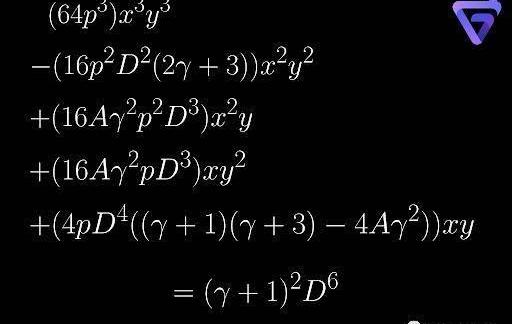
該函數的典型值圖如下所示：

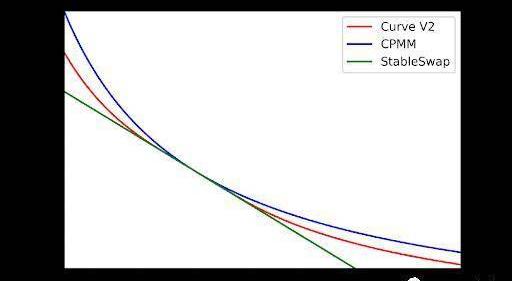
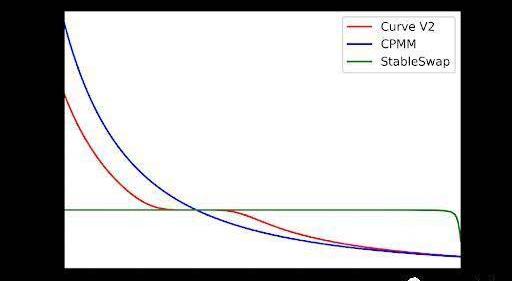
與CPMM和StableSwap相比，CurveV2的價格函數：

也可以繪制代幣x相對于代幣y的價格曲線。在平衡點(1000,1000)附近CurveV2價格函數恒定。與StableSwap相比，CurveV2略微延遲了價格變動，而不是完全延遲。與CPMM相比，隨著交易量的增加，價格開始以較小的滑點做出反應。總而言之，CurveV2在平衡點附近實現了非常小的滑點，并且在其他區域比CPMM實現了更好的滑點。至于其他非1的價格錨定，我們只需更改上面三次/六次方程中的_p_。因此，錨定價格的問題也解決了。

我們可以使用類似的在StableSwap中的牛頓法來計算交換結果。首先，我們根據池中當前的代幣數量計算_D_。其次，如果我們想換出代幣i，我們再次使用牛頓法來求解x?。同樣，x?的差異將是我購買的代幣數量。

為了確保多項式函數的根可以在設定的gas上限內求解，Curve白皮書討論了他們選擇的起始猜測，以及函數中的參數。他們使用一種稱為模糊測試的方法來確定這些最佳值。目前，我們不知道有關此方法的任何詳細信息，并且很想了解更多信息。

價格重錨過程：Xcp標準、EMA價格預言機、相對價格變化步長s：

為了確保小滑點，CurveV2通過改變價格標度不斷重錨做市商函數。然而，價格重錨可能導致流動性提供者承受價值損失。CurveV2引入了一個名為Xcp的變量來緩解這個問題：

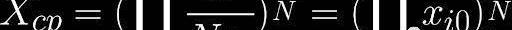
如果一次重錨后的損失大于累積的Xcp的一半，則該算法將保持做市商函數不變。有幾個問題我們想在未來回答，因為白皮書只簡要討論了Xcp。查看其源代碼可能會有所幫助。

Xcp值是否與用流動性池中當前代幣數計算出的價值成正比？存入或取出流動性是否計入Xcp？如果取出流動性計入Xcp，如果Xcp減少幅度過大會阻止取出流動性嗎？對于價格重錨，CurveV2使用EMA價格預言機來確定預言機價格。新的預言機價格向量由最近一次交易價格向量和前一個預言機價格向量的線性組合確定。新價格標度向量的變化方向與預言機價格相似，但不完全等于新預言機價格。他們通過引入相對價格變化步長s，將價格標度向量滯后于預言機價格。該方程可以使用歐幾里得幾何輕松導出。EMA價格預言機和價格標度延遲是為了減少近期價格波動的影響并更好地代表長期市場價格。

關于相對價格變化步長_s，根據我們“刷新Curve官網”的經驗，部分流動性池的s變化頻率至少為十分鐘的量級以上。CurveV2如何更新s_是一個有趣的問題，超出了我們當前知識的范圍。查看其源代碼也會有所幫助。

下面顯示了一個演示一次價格重錨過程的圖：

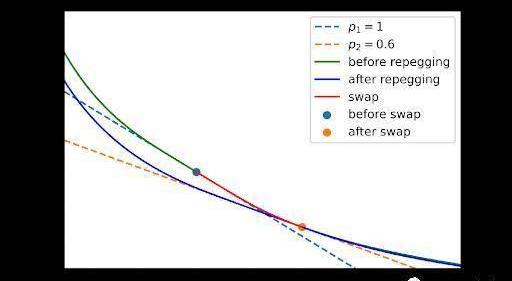
假設我們在x=1000開始我們的交易，并在x=1400結束我們的交易。最初，價格錨定于1。交易后，價格移動到0.6。為簡化起見，僅出于演示目的，我們將新的價格標度設置為與現貨價格相等，并求解六次方程以獲得_D_。現在做市商函數錨定于0.6，如上所示。

價格重錨本質上相當于找到一個新的做市商函數，該函數穿過當前代幣數量位置，在(x0,y0)處有一個平衡點，使得_y0/x0為等于(x0,y0_)處導數的絕對值。一個有趣的課題是獲取真實的Curve流動性池參數，做一個更好的價格重錨過程的演示。

聲音 | 雄安新區中級人民法院有關負責人：將推動區塊鏈等科技成果與司法工作深度融合:據河北法院網報道，5月10日，全國首個5G環境下的刑事案件三方遠程視頻庭審在河北雄安新區中級人民法院順利完成。雄安新區中級人民法院有關負責人表示，今后，雄安新區中級人民法院將充分發揮雄安新區技術資源和政策優勢，將智慧法院建設與雄安新區智慧城市建設一體規劃部署，積極推動5G、人工智能、大數據、區塊鏈等科技成果與司法工作深度融合，不斷提升審判質效，讓群眾享受到更高水平的司法服務。　　[2019/5/11]

CurveV2的動態交易手續費：

由于上面討論的CurveV2的做市商特性，將交易費用設為2級交易費用與動態權重的線性組合是合理的，衡量我們離平衡點有多遠。CurveV2選擇的_fmid和fout_值分別為0.04%和0.4%。下圖展示了2代幣池中的費用如何變化：

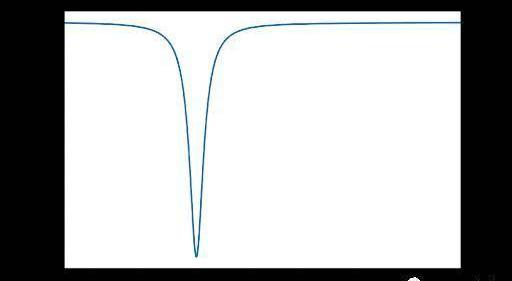
優點：做市商函數可以錨定于任何價格，適合所有代幣，而不僅僅是穩定幣。價格過渡比StableSwap更平滑。CurveV2還根據其內部的價格預言機不斷更新價格標度，以更好地代表市場價格，確保在平衡點附近交易。動態費用確保在此基礎上提供甚至更好的價格。

缺點：由于求解三次方程和六次方程，Gas費用可能會更高。僅根據其內部價格預言機進行價格重錨可能存在風險。我們想知道在通過_Xcp_標準時，是否存在價格標度與市場價格明顯不同的情況。如果是這種情況，與其他預言機交叉檢查價格可能會有所幫助。

Curve的StableSwap和動態錨定V2是為了使交易滑點盡可能小。StableSwap始終錨定于1，而V2使錨定價格跟隨市場價格。

下面將討論AMM算法的一些最新進展和可能的改進。

DEX聚合器：BalancerSOR算法的通用解決方案：

DEX聚合器是聚合現有AMM協議以實現更好交易結果的協議。如上所述，Balancer的SOR算法也適用于DEX聚合器，以確保數學上最優的交換策略。

Balancer的SOR算法的一般解決方案，沒有任何價格函數近似，可以表示如下：

因為價格函數可以是任何形式，具體取決于生成它們的AMM算法。這意味著滿足總代幣數量守恒和相等最終價格等條件的方程可能沒有解析解。

因此，我們引入了一種在機器學習等領域常用的技術，稱為梯度下降。我們將損失函數定義為不同價格函數值的方差。在選擇一個起始猜測后，我們可以迭代（通過損失函數相對于該變量的偏導數改變每個交換量，乘以學習率l)以獲得最佳結果，在一定的誤差接受范圍內。

由于作為最終等價函數的總交易量是單調的，因此該方法應該能夠找到全局最小值。同樣，上面的計算假設沒有簡單的解決方案。

Pivot算法：解決無常損失問題的一種嘗試：

Pivot算法試圖通過使做市商函數經過一個固定點(x0,y0)來對其進行樞軸旋轉。

(x0,y0)處的價格將始終是設計的當前市場價格Pt。這在概念上確保套利總是將流動性池帶回到點(x0,y0)。由于此功能，無常損失將為零。然而，實際上，該算法沒有足夠的參數來擬合當前儲備和。這意味著我們必須等待流動性池回到(x0,y0)，然后更改做市商函數。

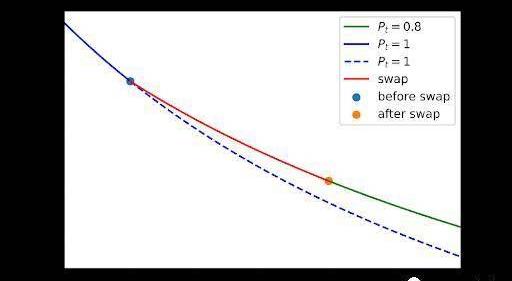
從上圖中我們可以看出，交易后的點不在新的做市商函數上。如果當前市場價格低于當前儲備的現貨價格，則流動性池也可能沒有任何動力回到(x0,y0)。

我們想知道是否存在這樣的函數通過(x,y)和(x0,y0)以及在(x0,y0)處的可調導數來適應市場價格。如果我們假設函數是凸的，那么市場價格不能小于這兩個點之間的線性段斜率。因此，如果做市商函數必須是凸函數，則此問題可能沒有完整的解決方案。

單邊流動性解決方案：

流動性提供者在存入流動性時可能不方便存入所有類型的資產。我想知道是否存在與Bancor采取的彈性供應方法不同的其他機制。直覺上，有兩種解決方案：1.首先使用相同的協議交換部分代幣2.無論如何存入單邊流動性，讓套利將價格帶回市場價格。

例如，我們希望將流動性存入一個等值的2代幣池中。

我們只有代幣x。不難計算我們需要交換多少，以便交換后每種代幣的價值相等。也很容易證明β總是在0和1之間，這意味著一個合理的結果。但是，交易后的價格可能與存入流動性時的價格不同。因此，我想知道協議是否真的將交換和流動性存入作為一項原子操作。進行交易時也存在價格滑點。到目前為止，Balancer和Curve等協議如何處理單邊流動性存入仍然是我們的一個問題。如果滑點很小，則進行上述操作是合理的。

BalancerandCurve白皮書中描述的第二種方法是是直接存入單邊流動性。這可能會大大改變價格。由此產生的套利也可能使無常損失變得重大。我們個人在Balancer白皮書和文檔中沒有看到任何懲罰措施。另一方面，Curve在存入單邊流動性時引入了一種稱為不平衡費的東西，其范圍從0%到0.02%。在現實中，由于套利和無常損失，在第二種方法下存入單邊流動性并沒有真正的動機。

下篇目錄

為CurveV2設計更好的動態權重17.當價格函數為非解析時應用價格范圍

Clipper：針對小額交易優化的AMM算法TWAMM：針對大額長期訂單優化的AMM算法TWAMM在恒定乘積做市商(CPMM)和對數市場評分規則(LMSR)上的應用TWAMM在YieldSpace等與時間相關的AMM上的應用結論和未來工作為CurveV2設計更好的動態權重：

γ值

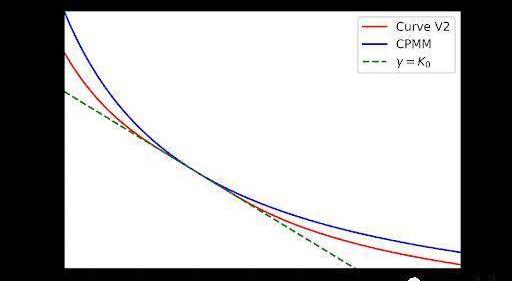
在CurveV2中，有一個常數稱為γ。如果我們也讓它動態化，會發生什么？例如，我們可以使它成為K0的函數。最簡單的情況是使其等于K0。這里的動機是讓函數在接近平衡點時表現得更像StableSwap，當函數遠離平衡點時，使其更像CPMM。

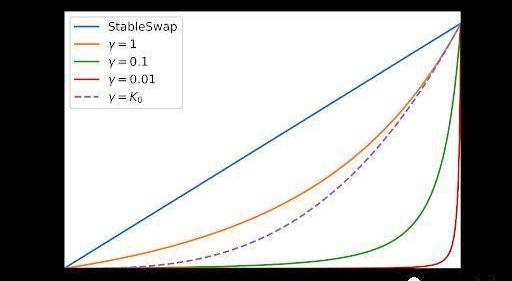
紫色虛線曲線位于StableSwap和小γ值曲線之間，應該為我們提供StableSwap和CurveV2之間的做市商函數。然而，當我們繪制做市商函數時，它的圖像跟StableSwap很相似：

??

這個問題有兩種解決方案：1.使A更小2.選擇K0的較高冪數來表示γ。兩者似乎都是可行的，然而1.破壞了A作為一個大數的目的：使做市商函數與價格錨定。我們進行的進一步測試似乎表明，更改A不會對函數行為產生影響。

第二種解決方案會使gas費用更高。K0的更高次冪數對應于我們需要求解的更高階多項式方程。事實上，CurveV2選擇動態權重K的特定形式的原因是為了模擬大指數K0的函數行為，同時不使多項式的階數更高。

?

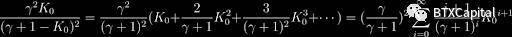
有趣的問題是：我們能否找到一個更好的動態權重來簡化我們需要求解的方程，同時保持與CurveV2相同或更好的功能？在設計這樣的動態權重時，我們還必須記住，我們需要在小滑點和做市商函數對預知市場未來的大訂單做出反應的能力之間保持平衡。顯然，只有價格錨定的StableSwap在這方面是行不通的，因為如果錨定價格與市場價格不同，幾乎所有的代幣都會被買斷。只有在保持這種平衡的情況下，價格重錨才可行。

當價格函數為非解析時應用價格范圍：

我們可以將價格范圍概念應用于CurveV2。由于沒有關于池中代幣數量的價格解析表達式，我們需要擬合價格和代幣數量之間的關系。應用于做市商函數的偏移量由價格范圍決定。編寫這樣的程序可以使資本效率更高。

Clipper：針對小額交易優化的AMM算法：

Clipper13使用最適合小額交易需求的AMM算法。它將恒定乘積做市商(CPMM)和恒定總和做市商(CSMM)概括為兩個極端情況。

Clipper13：NewInvariantsforAutomatedMarketMakinghttps://github.com/shipyard-software/market-making-whitepaper/blob/main/paper.pdf

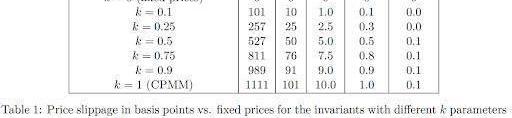
當只有兩種類型的代幣時，不變量可以簡化為更簡單的形式，其中x0和y0是初始流動性提供者設置的代幣數量。以下是流動性池在不同k值下的行為。x和y軸由x0和y0歸一化。

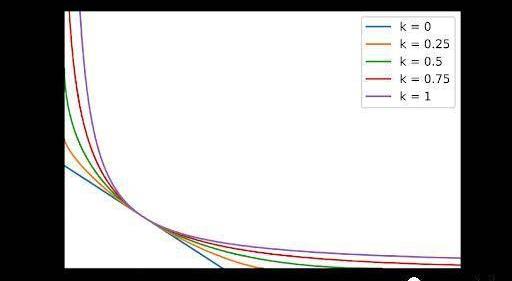
較小的k值對應于(1,1)附近的較低滑點。當k介于0和1之間時，不變函數可以與x和y軸相交。這意味著池中的代幣可能會售罄。該交叉點的價格為零，這意味著該價格在轉折點之前優于CPMM價格。過了轉折點后，CPMM的價格比較好。這可以在下圖中說明：

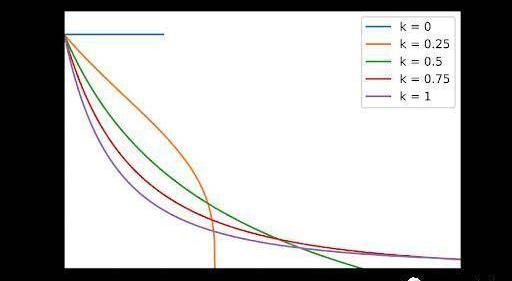
再次對x軸進行歸一化。隨著我們遠離初始點(1,1)，X代幣相對于Y的價格下降。我們可以精確計算交點發生的位置：

優點：通過引入k，Clipper在交易量較小時實現了更低的滑點。Clipper白皮書中的以下圖表進一步證明了這一點。

FromClipperwhitepaper

缺點：當交易量超過一定門檻時，價格會明顯低于CPMM。

為了保證更好的價格，算法必須不斷地價格重錨以保持當前池儲備接近(1,1)點。它可以使用與Curve相同的機制。該算法通過遵循其跟蹤市場價格的內部價格預言機進行價格重錨。本質上，這等價于求解下面的公式，但這次x,y是已知的。P由價格預言機給出。最后求解x0的這個方程給了我們新的平衡點。

這確保我們始終以較小的滑點接近市場價格進行交易。目前我們還沒有調查Clipper是否實現了這一點，因為這在Clipper白皮書中沒有解釋。需要進一步查看其源代碼。

價格范圍概念也可以應用于Clipper：

TWAMM：針對大額長期訂單優化的AMM算法：

在上面討論的所有AMM中，我們一次只能在一個方向上進行交易。如果我告訴您最近出現了一種允許同時進行雙向交易的算法呢？

TWAMM1?算法將一段時間內的長期訂單轉換為無限小的虛擬訂單的積分。訂單可以兩邊同時進行。此外，在同一時間范圍內、同一交易方向執行的訂單會匯集在一起以簡化計算。因此，一段時間內的長期訂單以等于該時期時間加權市場價格的價格執行。

TWAMM1?https://www.paradigm.xyz/2021/07/twamm/截至目前，只對于兩種類型的AMM，CPMM和LMSR存在解析形式的TWAMM解。

讓我們考慮一般情況，在一段時間內，代幣X的總銷售額為xin，Y的總銷售額為yin。X的賣出率為_f(t)_，Y的賣出率為g(t)。從時間t到_t_+_dt_代幣X數量的凈變化可以計算為代幣X的銷售數量減去在此期間購買的代幣X數量，匯率為dy/dx。由于在此期間代幣Y的銷售量無限小，因此可以使用現貨價格作為實際匯率。

因此，我們得到一個非線性一階微分方程。取決于dy/dx、_f(t)_和g(t)的形式，方程可能有也可能沒有解析解。

TWAMM在恒定乘積做市商(CPMM)和對數市場評分規則(LMSR)上的應用：

當應用于CPMM時，方程可以被積分，如果f(t)/g(t)是一個常數，這意味著代幣X和Y的銷售策略是相同的。我們可以進一步簡化表達式：

存在這個積分的解析表達式。利用雙曲函數的性質，我們可以得到一個漂亮的最終解，它只取決于池的原始位置__和_xin，yin_。由于CPMM的做市商函數關于_x_和y完全對稱，因此也可以通過在xend的最終表達式中交換xin和yin、x0和y0的位置來表示最終的代幣Y數。代幣X數和代幣Y數的乘積正如預期的那樣等于k。

這種源自CPMM的微分方程形式，實際上有一個數學名稱叫做“Riccati方程”。Riccati方程的一般形式如下：

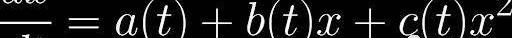
Riccati方程沒有一般的解析解。但是，存在可以求解Riccati方程的特殊情況。有一篇論文1?討論了這些案例。如果Riccati方程的系數滿足這個條件：

論文1?：AnalyticalsolutionsoftheRiccatiequationwithcoefficientssatisfyingintegralordifferentialconditionswitharbitraryfunctionshttps://arxiv.org/abs/1311.1150

則Riccati方程可以轉化為Bernoulli型方程。Bernoulli型方程可以很容易地求解。這應該給我們與以前相同的結果。從上面我們可以看出，滿足這個條件與保持f(t)/g(t)恒定相同，這是我們在第一種求解微分方程的方法中假設的。

當_f(t)/g(t)_不是常數時，我們可以選擇什么形式的_f(t)_和_g(t)_使微分方程具有解析解仍然是一個懸而未決的問題。找到這樣的解決方案會給我們更多的選擇。

現在讓我們將TWAMM應用到LMSR：

同樣，我們假設銷售策略是相同的。然后可以對微分方程進行積分。我們可以進一步簡化最終的代幣X和Y數量表達式為：

同樣，當銷售策略不同時，也不能保證微分方程具有解析解。

一旦我們獲得了_xend_和_yend_，我們就可以計算出每方將收到多少代幣X和代幣Y：

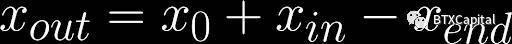
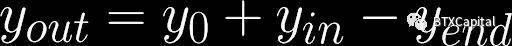
由于在此期間，同一交易方向的所有訂單都匯集在一起。每個個體交易者將根據他對_xin_和_yin_的貢獻比例獲得他應得的代幣份額。

優點：TWAMM通過允許交易對手同時對這些大訂單進行交易，從而使大訂單的價格滑點更小。在最理想的情況下，可以實現零滑點交易。在這種情況下，_xend_=x0，_yend_=_y0_，TWAMM可以理解為充當了訂單簿，在不提供流動性的情況下在雙方之間交換代幣。長期訂單被分解成無限小的訂單，這些訂單在區塊之間虛擬執行。由于這種性質，它不太容易受到三明治攻擊，因為攻擊者必須在塊的末尾放置一個命令，并在下一個塊的開頭放置另一個命令。

缺點：如果我們允許訂單在任何時候到期，gas費用可能會非常高。這是因為我們必須多次計算積分結果。在最壞的情況下，我們必須計算每個塊的結果。因此，在實踐中我們必須讓訂單在某些區塊到期以簡化計算。此外，TWAMM使用的流動性池必須與現有的流動性池不同，因為沒有虛擬訂單和懶惰計算的概念。普通交易者在與TWAMM交互時不想支付懶惰計算產生的額外gas費用。

TWAMM在YieldSpace等與時間相關的AMM上的應用：

我們還可以將TWAMM應用于與時間相關的AMM，例如YieldSpace1?：

YieldSpace1?：AnAutomatedLiquidityProviderforFixedYieldTokenshttps://yield.is/YieldSpace.pdf

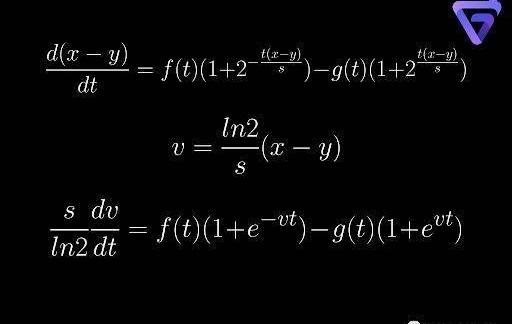
做市商函數有兩種形式，這兩種形式都會導出目前我們不知道如何求解的微分方程。在第二種形式的情況下，微分方程可以簡化為單個微分方程。

結論和未來工作：

我們希望這篇綜合性的、介紹性的、學習筆記風格的論文能夠為對AMM算法一無所知的人和有更多經驗的人提供一些見解。

總而言之，AMM算法的核心基本上是關于做市商函數的設計及其曲率分布的操縱。顯然，我們需要閱讀另一篇GuillermoAngeris和TarunChitra寫的論文1?，其中詳細討論了這一點。除此之外，還有高效的價格解決方案和高效的流動性提供解決方案。最近的TWAMM算法闡明了我們如何使用AMM算法來實現中心化交易中常見的訂單簿類型的撮合。我們相信AMM算法的未來將更接近訂單簿風格。

GuillermoAngeris和TarunChitra寫的論文1?：ImprovedPriceOracles:ConstantFunctionMarketMakershttps://arxiv.org/abs/2003.10001至于未來的工作，我們計劃對本文中提到的一些問題進行更深入的挖掘。這包括閱讀論文、、、、，推導其他AMM的無常損失公式，推導其他AMM的流動性分布，了解模糊測試的工作原理，回答我們提出的關于Xcp的3個問題，更多地了解如何選擇最有效的價格預言機和s值，制作Curve價格重錨過程的動畫，了解更多關于單邊流動性的創新，嘗試設計更好的動態權重K，將價格范圍應用于其他AMM，將TWAMM應用到其他AMM并找到更多解析解。

作者感謝FangyuanZhao、ShowenPeng、DW對本文研究課題提出十分有用的意見。作者還要感謝火幣研究院的LianxuanLi。作者特別感謝Paradigm的DaveWhite和DanRobinson邀請加入TWAMM討論組以及他們富有洞察力的討論。同時也要感謝BTXCapital的VanessaCao和JaneHu對本文的翻譯和排版。

Tags：SWAPAMMCurveCURMSWAPBonded dAMMRENBTCCURVE價格curve幣價格

聚幣