ROT:密碼專欄 | 超強進階：PLONK VS Groth16（下）_Protekt Protocol

前言

本篇是“PLONKVSGroth16”的下篇，在上篇中我們對PLONK作了簡要介紹，分析了PLONK和Groth16算法在「可信驗證」和「約束構建」上的異同。那么，接下來讓我們一起看看在后續的「證明生成」和「驗證階段」兩者將有怎樣的差異，以及整體上的性能區別。

證明生成

對于程序qeval,prover需要證明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5

在上篇中我們已經介紹了PLONK的約束形式：門約束與線約束。繼續使用之前的例子，約束意味著零知識證明系統將這個問題約束成了一組格式固定的數學表達式，即問題描述等價于約束描述。而如果證明者真的知道這個問題的答案，將答案和計算中的中間參數代入約束表達式，這個組表達式必將是成立的。反之，如果該Prover提供的一組解無法使表達式成立，說明prover并不具備關于該問題解的知識。

IoTeX密碼學負責人Xinxin Fan博士被IEEE標準協會正式任命為P2418.4標準工作組副主席:官方消息，物聯網區塊鏈平臺IoTeX密碼學負責人Xinxin Fan博士被IEEE標準協會正式任命為P2418.4標準工作組——“區塊鏈技術在物聯網領域應用”副主席，該工作組致力于創建區塊鏈技術在物聯網（IoT）使用中的通用標準。

范博士將代表IoTeX與IEEE 2418.1標準工作組主席兼IEEE區塊鏈計劃聯合主席Ramesh Ramadoss博士一起工作，共同推動物聯網區塊鏈行業標準制定，目前加入該標準工作組的企業來自華為、思科、AMD、IBM、GE、戴爾等。這是IoTeX繼擔任IIC區塊鏈工作組聯合主席之后的又一標準制定的重要任命。

IEEE 全稱為「電氣和電子工程師協會」（Institute of Electrical and Electronics Engineers），成立于1884年，是目前全球最大的非營利性專業技術學會，致力于推動世界領先技術標準造福人類，在全球范圍內具有極大的權威性和影響力。[2021/5/7 21:34:08]

這是最樸素的證明驗證思路，可以將它看作是“鎖”和“鑰匙的配對“：該問題約束的構建類似于“打造門鎖“，而針對該問題提供的一組解信息就是”一把開啟門鎖的鑰匙“。顯然，Prover可以舉著自己的解交給驗證者來驗證。可是這違背了我們的零知識原則：Verifier不應該獲取到Prover的隱私信息。

全國密碼創新大賽為獲獎團隊頒發數字人民幣獎金138萬元:10月26日，“金融密碼杯”2020全國密碼應用和技術創新大賽頒獎在蘇州舉行。央行副行長范一飛及評審指導小組成員為獲獎團隊頒發了數字人民幣獎金，獲獎團隊來自建信金融科技公司、北京郵電大學等，由此計算此次共發出數字人民幣獎金138萬元。（21世紀經濟）[2020/10/27]

那么有什么方法能在解鎖的同時保護隱私信息呢？

這里我們用到一個簡單的數學小技巧：減除，對此不太了解的讀者可查閱文章最后的前置知識。在前文《超強進階：PLONKVSGroth16》我們已經對從約束系統轉化到多項式進行了詳細的描述，在此我們不再贅述具體的轉化過程，但需要重復的一點是：根據生成時使用的點值對，生成的多項式在這些點處的取值將恒為0。PLONK同理，此處我們給出兩種算法的約束系統轉化為多項式后的形式。

Groth16:

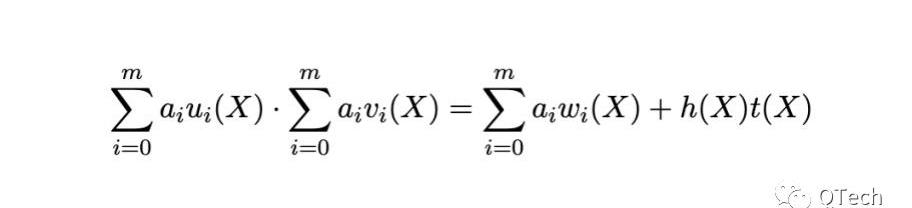
V神：密碼學在制造可擴展區塊鏈很有價值:9月26日消息，V神在推特上分享了理想矢量“ideal vector”開放鏈接，并認為“ideal vector對制造可擴展區塊鏈很有價值。V神透露，如果包含“ideal vetor”的內容，eth2.0將會變得更好。[2020/9/26]

PLONK:?我們設門約束多項式為D(X)，線約束多項式為L(X)，那么PLONK的整個約束多項式將被表示為：

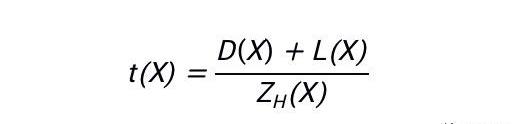
可以看到，兩者都使用了減除的思路，也就是這里的h(X)和ZH(X)，其具體內容取決于構建約束多項式時取的點值。

證明與驗證

同樣在之前的文章中，我們可以看到Groth16的證明規模極小，只包含三個群元素A,B,C。然而，這樣優雅的證明實現依賴于它的非通用可信設置，這也是Groth16的一大痛點。在Groth16中，證明方提供A，B，C，驗證方基于可信設置提供的參數，構建一個配對驗證等式。在驗證過程中包含了三次配對操作，也就是對驗證性能影響較大的耗時運算。Groth16的具體證明驗證如下所示。

動態 | 工信部成立密碼應用研究中心，推動密碼應用與創新發展:1月19日，工業和信息化部召開部密碼應用研究中心（下稱“中心”）成立大會，工信部黨組成員、副部長陳肇雄和國家密碼管理局副局長何良生共同為中心揭牌。中心的成立，是工業和信息化部貫徹落實《中華人民共和國密碼法》、推動密碼應用與創新發展的重要舉措。中心將緊緊圍繞黨和國家戰略需求，致力于增強密碼原始創新能力，強化科研供給側與應用需求側對接，深入推進與部屬高校密碼學院協同創新，與相關部屬單位密碼力量融合發展，努力建設成為密碼創新發展高地，為促進工業通信業高質量發展、加快制造強國和網絡強國建設提供有力保障。[2020/1/22]

Groth16證明：

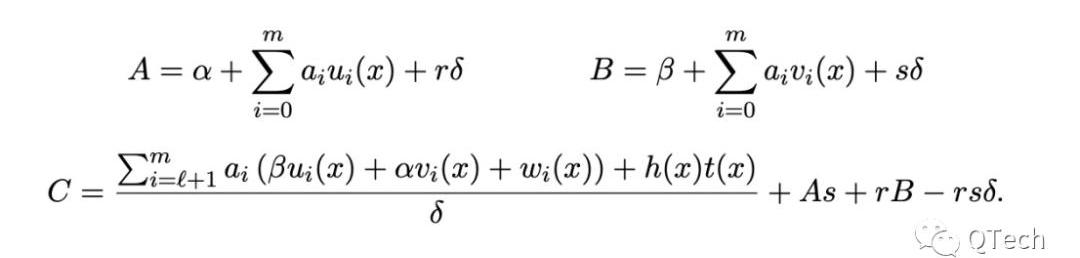
Groth16驗證：

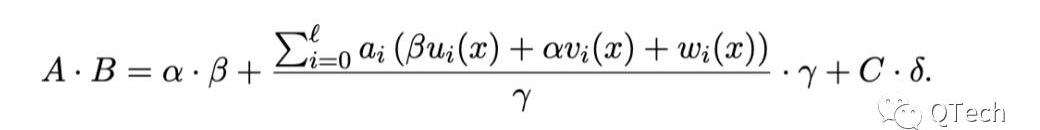
密碼學之父：不管每個人擁有多少的財富都會想要去貢獻自己所擁有的價值:在2018分散經濟討論會上， 密碼學之父David Chaum發表演講稱，不管每個人擁有多少的財富都會想要去貢獻自己所擁有的價值。盲簽名是一種只需要數字就能收款的具有革新價值的想法，類似于比特幣和以太幣等虛擬貨幣，以區塊鏈為基礎的技術可以確保收款人和匯款人的匿名性，加密學幫助了人們的日常生活，希望日后可以共享、分享信息，更進一步可以直接以民主的方式開創可能性。[2018/4/3]

相比之下，PLONK的證明驗證將會復雜得多，這也是使用通用可信設置付出的代價。從驗證方角度看，由于可信設置參數缺少了包含問題具體內容，從而無法幫助其構建一些制約證明多項式的值。因此，如何固定住證明多項式的內容成為一個難題。PLONK使用的一個思路是引入Kate承諾。

結合前述的約束多項式，我們可以對t(x)中出現的每一項都構建一個承諾，以實現驗證方的驗證。PLONK證明的具體內容如下，包含了兩個點處的驗證：Wz(X)為多個多項式的同點承諾，Wzw(X)則為另一個點處的對z(X)的承諾。

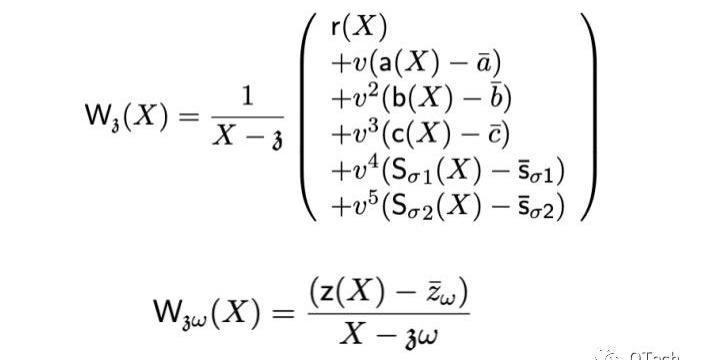
最后，PLONK的驗證在原文中也被歸納為一個簡潔的公式，實際上就是將上面提到的兩個點處的承諾簡單相加，具體等式如下所示：

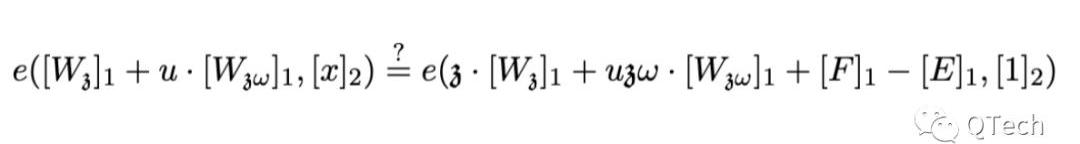
以上就是PLONK和Groth16算法內容的具體對比結果，講了這么多冗長的公式變換，兩者在性能層面的差距究竟如何呢？

性能比較

在這里我們給出的是PLONK論文中的結論。Table1是在證明階段的一個性能比較，Table2則是驗證階段的性能。可以看出，在驗證上，兩者的差距不大，Groth16比PLONK多了一次配對運算；而在證明方面我們遺憾地發現，Groth16不論在證明的工作量還是證明長度上仍然保持著最優的性能。但需要指出的是PLONK，尤其當它工作在fast模式時，所使用的SRS長度是所有算法中最短的。

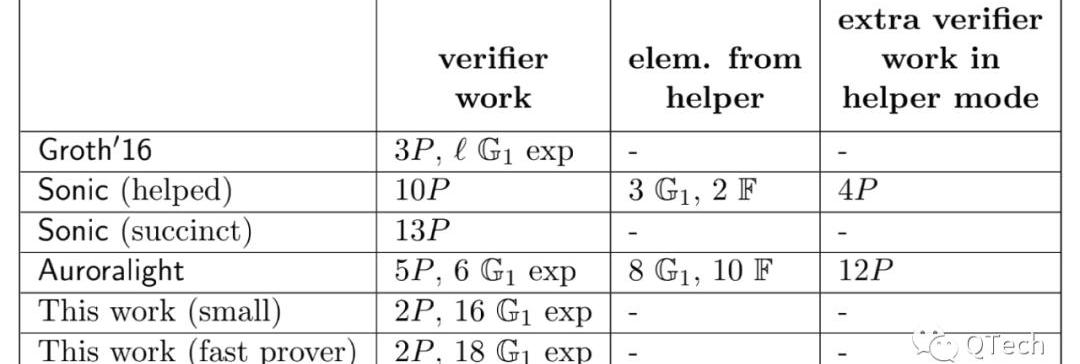
▲驗證階段性能比較

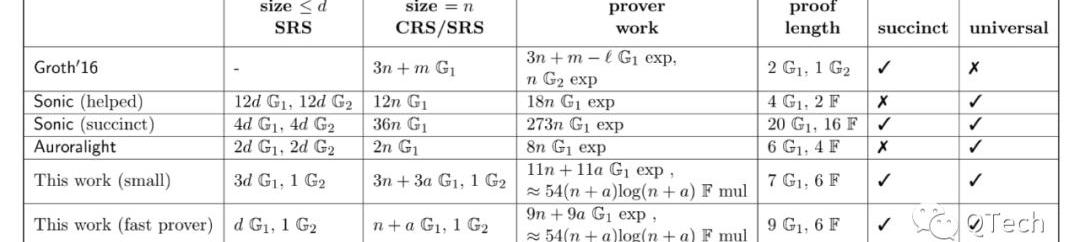
▲證明階段性能比較

前置知識

多項式減除

顧名思義，化減為除：若我們需要證明一個多項式f(x)在點a的取值為b，也就是證明f(a)-b=0；那么我們可以將其轉換為證明多項式f(x)-b可以整除(x-a)。其數學表示：

設多項式f(x)且f(a)=b，則存在一個多項式g(x)，使得：f(x)-b=g(x)(x-a)

kate承諾Kate承諾是由Kate，Zaverucha和Goldberg在2010年提出的一種多項式承諾方案。Kate承諾有多種形式，本文僅介紹PLONK中使用的常用形式，詳細可參考其paper中的相應內容。其常用形式可以概括為對多項式的隱藏和部分打開驗證。針對多項式f(x)，Kate承諾的具體步驟如下：

1）構造f(x)在點a處的承諾C

C：f(a)

2）選取點z，執行f(z)的opening

gz(x)=f(x)-f(z)/x-z

wz=gz(x)

3）給定f(z),C和Wz，驗證Kate承諾

C=wz*(a-z)+f(z)

以上就是“PLONKVSGroth16”的全部內容，如有任何疑問，歡迎添加小助手桔子加入技術交流群，在這里，你想知道的都會得到解答～

A.Kate,G.M.Zaverucha,andI.Goldberg.Constant-sizecommitmentstopolynomialsandtheirapplications.pages177–194,2010.

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.2019.

Tags：PLOLONGROROTPlow Finance3X Long Cosmos TokenFGROW價格Protekt Protocol

歐易交易所app官網下載