GRO:【密碼專欄】超強進階：PLONK VS Groth16（上）_Biskit Protocol

前言

前文《天冷了，干了這碗“零知識證明”雞湯》對「零知識證明學習」作了一個形象化的比喻：燉雞湯。那么本系列的主要內容可以簡單概括為《論高壓鍋燉雞湯的一百種方法》之方法二。在學會了“清燉雞湯”之后，不如來一口“阿膠雞湯”補補腦細胞吧！

正如雞湯不同風味之間各具千秋，不同的zk-SNARK方案也各有所長。zk-SNARK方案可以被分為與zk-SNARK，PLONK與Groth16分別是其中的典型代表。通過本系列，我們將對PLONK算法內容作簡要介紹，并指出PLONK和Groth16算法思路上的異同。

PLONK算法在中提出，由來自于ProtocolLabs的研究員Gabizon和以太坊隱私交易協議AztecProtocol的兩名研究人員合作完成。PLONK的提出晚于Groth16，在證明和驗證的性能上與Groth16也存在一定差距，但是基于通用可更新的可信設置這一特點，使PLONK算法在零知識證明領域占據了一席之地。

可信設置

可信設置可以說是PLONK和Groth16兩者間最顯著的差異。正是為了避免一次性的可信設置，PLONK設計了后續的約束系統和問題壓縮方式。那么什么是零知識證明中的可信設置呢？可信設置實際上是在創建一個用于證明驗證的秘密，任何知道這個秘密的人都可以偽造證明通過驗證。如果將零知識證明看作是一扇擋在證明者a和驗證者b之間上鎖的門，那么合法構建的證明就是可以打開門的口令，a提供口令即可進入房間。但是如果a得知了門的秘密也就是房間窗戶的位置，那么a可以直接無視鎖的存在翻窗進入房間。

?馬斯克：公司繼續大量購買英偉達的GPU:金色財經報道，特斯拉CEO馬斯克表示，當前宏觀經濟環境仍然具有不確定性；預計將于第三季度舉行Cybertruck交付活動；最好還是按更低的價格大量發貨；現在是進一步擴大公司領先優勢的好時機；公司繼續大量購買英偉達的GPU。[2023/4/20 14:14:46]

▲無窗的房間

顯然，最安全的做法是找一個「沒有窗的房間」，這也是一部分零知識證明方案的思路——無需可信設置，例如可擴展透明知識論證zk-STARKs和防彈證明Bulletproofs。雖然它們的安全性得到提高，但是目前這類方法的證明驗證性能是遠低于zk-SNARKs的，近線性的驗證和規模較大的證明使其不適用于很多場景。

▲窗戶位置指定策略

PLONK和Groth16的做法都是保留窗戶，但是盡力保護窗戶的位置不被別人知道。

Groth16的做法是：根據不同的問題，每次都指定窗戶在房間中的擺放位置，也就是它需要一次性的可信設置。而PLONK面對不同的問題時：窗戶的位置是固定不變的，即窗戶的位置只需要被指定一次。也就是說PLONK的可信設置是通用的。那么這些窗戶指定的位置由誰來確定呢？當然，可信第三方是一個備選項。但這意味著說這間房間是否會被惡意證明者攻破，其安全性寄希望于這位第三方。除此之外還有一項熱門技術也可為其提供思路——多方安全計算。沿用之前的例子，可以不太嚴謹地將MPC概括為：多個人共同指定窗戶的位置，除非這些參與者全部聯合起來對答案，這個位置將無法由任何人得知。

APT短線漲至9.85 USDT，24H漲幅為31.4%:金色財經報道，行情顯示，Aptos（APT）短線漲至9.85 USDT，現報9.7786 USDT，24H漲幅為31.4%。[2022/10/23 16:36:04]

顯然，使用MPC時，參與者的數量越多，秘密的安全性越高，這類可信設置也比可信第三方更為用戶所接受。遺憾的是，雖然目前提出了基于Groth16的可信設置，但是由于Groth16的秘密計算與特定的問題相關聯，每次遇到新的問題時，必須重新開啟一輪MPC可信設置。可想而知，需要多方參與的計算協議將是極為繁瑣的，這樣將大大影響Groth16的性能。相比之下，具備通用性的PLONK與MPC的適配度極高。

而之前提到的PLONK可信設置的可更新性則是指：通用的PLONK秘密可以通過再開啟一輪MPC作更新。新生成的秘密安全性建立在兩次MPC的安全性上，只要兩次中有一個參與者是誠實的，這個秘密就是可信的。約束系統

Groth16及PLONK均將程序先轉化為一個由加法門和乘法門組成的算術電路，再通過將電路構建為多項式的形式來進行后續的計算。本節我們將使用Vitalik文章中的一個簡單例子進行說明：

對于程序qeval,prover需要證明自己知道qeval(x)=35的解，即x=3。

研究：加州是對比特幣和以太坊最感興趣美國州:金色財經報道，CoinGecko近日發布了一項研究，確定美國對比特幣和以太坊這兩種主要數字貨幣最感興趣的十大州。在2022年5月2日至8月21日期間，CoinGecko團隊利用CoinGecko的頁面流量數據進行統計。研究發現，加利福尼亞州在美國所有州中占主導地位，伊利諾伊州的指數得分第二高。前十大州還包括紐約州、佛羅里達州、華盛頓州、賓夕法尼亞州、德克薩斯州、弗吉尼亞州、喬治亞州和亞利桑那州。（Bitcoin.com）[2022/9/5 13:09:33]

defqeval(x):

y=x**3

returnx+y+5，其轉化為算術電路可表示如下：

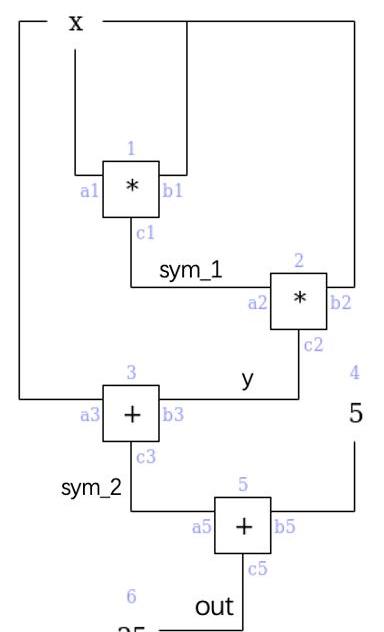
PLONK中，上圖電路的描述由兩部分組成：門約束與線約束。門約束固定電路中每個門的動作。此外，在電路中我們規定相連線的值應保持一致，對此線約束規定這些線的關系。接下來我們分別討論兩類約束的多項式表示。門約束

在PLONK中，對于第i個門，可被描述為如下形式：

QiDao團隊將Stablecoin MAI添加至Polygon網絡Aave V3的提案已獲通過:8月29日消息，Polygon 原生 Stablecoin 協議 QiDao Protocol 團隊于 Aave 社區發起將 QiDao 推出的 Stablecoin MAI 添加到 Polygon 上的 Aave V3 的提案已獲通過，該提案建議風險參數設置為 75% 的貸款利率、80% 的清算門檻、10% 的儲備系數、每條鏈 200 萬美元的初始債務上限。[2022/8/29 12:54:58]

（QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+Qci=0

其中Q均為常數，a,b,c則是信號的下標。具體地，在PLONK中門約束可以被分為三類：算術約束、布爾約束、公共輸入約束。

最為常見，用于表示電路中的所有加法門和乘法門，此時a,b,c分別表示門的左右輸入和輸出信號下標，Q_C一般為0。根據門的類型剩余的符號有不同的取值：

加法門：QLi=1，QRi=1，QOi=-1，QMi=0??ai+bi-ci=0乘法門：QLi=0，QRi=0，QOi=-1，QMi=1-ci+?aibi=0

基于Substrate構建的Creditcoin 2.0已上線:6月27日消息，基于Substrate構建的Creditcoin 2.0已于6月23日上線。新Creditcoin協議明顯提高網絡性能，并利用Credal API促進在現實世界中的應用。

據悉，通過公開記錄信貸歷史，Creditcoin減少借款人和貸款人之間的信息不對稱，有助于確保資本融資，建立信貸歷史，并促進新興市場金融客戶和企業之間的信任。[2022/6/27 1:32:53]

顧名思義，用于約束布爾類型的信號，其值只能取0或1。例如現在需要約束下標為j的信號∈{0,1}，那么門約束式子中各變量的取值為：

ai=bi=j，QLi=-1，QMi=1，QOi=QRi=Qci=0

-j+j*j=0

另外，針對問題中出現的證明方和驗證方都知道取值的輸入，需要在約束系統中有所體現。例如要求約束下標j的信號取值為v，對應的取值為：

ai=j，QLi=1，QMi=QOi=QOi=0，Qci=-v

j-v=0

利用該式，我們可以很容易地表示上圖中的所有門約束：

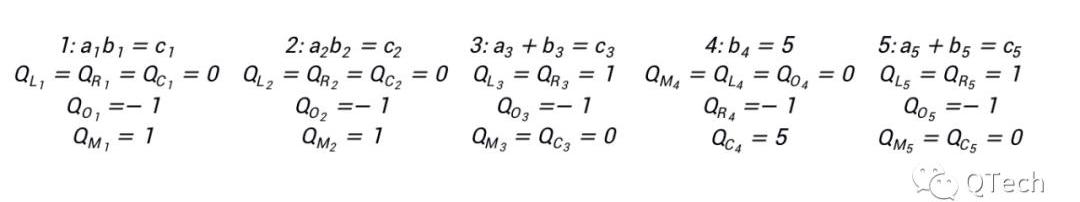
與Groth16類似，可以將所有的多項式組整合在一個多項式中：

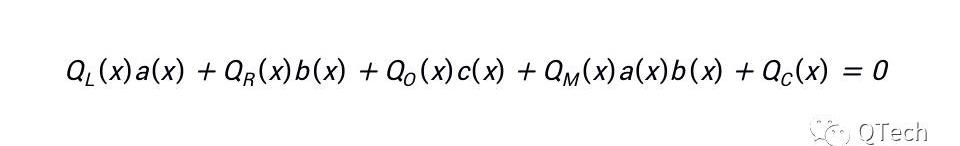
線約束

線約束可以分為兩種情況：

同一多項式內部，例如：a1=a3

不同多項式之間，例如：a1=b1

當只需要考慮情況1時，可以通過構造p(x)=P(x)來實現約束：

X(X)=X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

其中β,γ為隨機數，X->Y表示了待約束的多項式，P(x)使用了x的置換σ(x)。對于下面例子：

X(1)→Y(1)

X→Y：X(2)?→?Y(2)?and，Y(1)=Y(3)

X(3)→?Y(3)

σ(1)=3

σ(X)：σ(2)=2

σ(3)=1

當且僅當Y(1)=Y(3)成立時，p(x)=P(x)。

現在，讓我們增加問題的復雜度：需要約束的多項式個數為k時。自然地，設門的總數為n，我們可以對第j個多項式構造對應的p_j(x)=P_j(x)，即

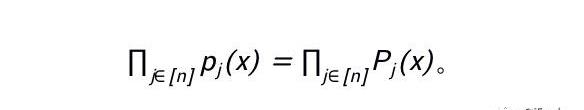
進一步地，情況2的出現要求對以下情況中的x作區分：

pj(x)and?pi(x)????

那么可以增加對x的映射，對于第j個多項式：

X(X)=(j-1)*n+X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

以上就是線約束的全部內容，其實質是為了保證電路中同一條或相連線上的值相等。

與Groth16類似，將上述的約束聯立將得到一個完整的PLONK約束系統。通過將抽象的代碼和電路轉化為約束系統R1CS，我們可以將一個零知識證明問題固定下來。讓我們帶著問題進入下篇：PLONK中如何將R1CS轉為多項式描述？它與Groth16做法區別在何處？敬請期待！

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.(2019).PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.

SeanBoweand?ArielGabizonandIanMiers.(2017).ScalableMulti-partyComputationforzk-SNARKParametersintheRandomBeaconModel.

https://vitalik.ca/general/2019/09/22/plonk.html

Tags：LONPLOROTGROpoloniex無法提現PlotXBiskit ProtocolGRO幣

LTC