ITA:Vitalik Buterin：協議設計中的封裝復雜性和系統復雜性權衡_VITA

作者：VitalikButerin，原文來源：vitalik.ca?

以太坊協議設計的主要目標之一是最小化復雜性：使協議盡可能簡單，同時仍然使區塊鏈能夠完成一條有效區塊鏈需要做的事情。以太坊協議在這方面遠非完美，尤其是因為它的大部分是在2014-16年設計的，當時我們對它的了解要少得多，但我們仍然盡可能地積極努力降低復雜性。

然而，這一目標的挑戰之一是復雜性是難以定義的，有時，您必須在兩種選擇之間進行權衡，這兩種選擇會引入不同類型的復雜性并具有不同的代價。我們如何比較？

允許對復雜性進行更細致入微的思考的一種強大的智力工具是區分我們稱之為封裝復雜性和系統復雜性的東西。

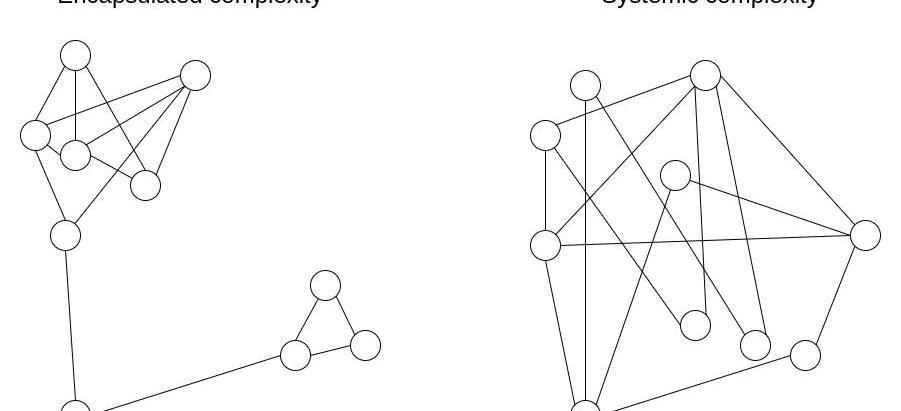
當一個系統具有內部復雜的子系統但對外提供一個簡單的“接口”時，就會出現封裝復雜性。當一個系統的不同部分甚至不能完全分開并且彼此之間具有復雜的相互作用時，就會出現系統復雜性。

Blur推出Global Activity界面，可監控所有NFT系列的上架和銷售活動:金色財經報道，NFT 市場 Blur 宣布推出可監控和跟蹤所有 NFT 系列上架和銷售活動的 Global Activity 界面，同時允許用戶自定義監控多個 NFT 系列的活動。[2023/4/21 14:17:52]

下面有一些例子。

BLS簽名與Schnorr簽名

BLS簽名和Schnorr簽名是可以用橢圓曲線制作的兩種流行的加密簽名方案類型。

BLS簽名在數學上看起來非常簡單：

簽署：

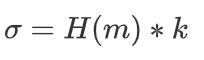
驗證：

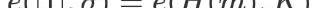
4萬枚ETH從Vitalik Buterin創建的合約地址轉出:11月24日消息，據WhaleAlert監測，4萬枚ETH從Vitalik Buterin創建的合約地址（0x22086開頭）轉出，該合約地址當前還持有逾25萬枚ETH，價值近3億美元。[2022/11/24 8:05:12]

H是一個哈希函數，m是消息，k和K是私鑰和公鑰。到這里為止，看起來都很簡單。然而，真正的復雜性隱藏在e函數的定義中：橢圓曲線配對，這是所有密碼學中最難理解的數學題之一。

現在，再看看Schnorr簽名。Schnorr簽名僅依賴于基本的橢圓曲線。但是簽名和驗證邏輯要復雜一些：

那么......哪種類型的簽名“更簡單”？這取決于你關心什么！BLS簽名具有巨大的技術復雜性，但復雜性都隱藏在e函數的定義中。如果將e函數視為黑盒，BLS簽名實際上非常簡單。另一方面，Schnorr簽名的總體復雜性較低，但它們有更多可能以棘手的方式與外部世界交互的部分。

聲音 | Kavita Gupta：風投在加密貨幣領域的投資方式發生了變化:ConsenSys Ventures創始執行合伙人Kavita Gupta在最近接受采訪時表示，風投在加密貨幣領域的投資方式發生了變化。風投開始適應新的模式，加密貨幣投資比較獨特，其流動性、持續性、風險特征、波動性等因素都與傳統的長線投資基金有很大不同。區塊鏈投資者的構成在不斷變化，企業家畫像也在變化。在這一領域擔任CEO的人士從大部分是年期的技術專家變成了很多是經驗豐富的工程師和連續創業者。產品的愿景、路線圖，尤其是接納的理由和友好的用戶界面已成為了討論主題之一。一些大型風投公司正在成立加密貨幣領域專用基金，使世界更加接近Web 2.0和Web 3.0，并驗證這一領域的許多早期技術，而這些技術在一年前還看起來可能是不現實的。”[2019/1/30]

例如：

進行一個BLS多重簽名很容易：只需

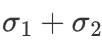
聲音 | V神：郵箱Vitalik@butterin.me不是我的:以太坊創始人V神（Vitalik Buterin）發推表示，“Vitalik@butterin.me不是我的，任何由這個郵箱發出的郵件都是騙子所為。我的所有郵箱地址都是.com或者.org這兩個域名。”[2018/11/1]

。但是Schnorr多重簽名需要兩輪交互，并且需要處理棘手的密鑰取消攻擊。

Schnorr簽名需要隨機數生成，BLS簽名不需要。

橢圓曲線配對就像是一個強大的“復雜性海綿”，因為它們包含大量封裝的復雜性，但可以實現系統復雜性低得多的解決方案。在多項式承諾領域也是如此：將KZG承諾的簡單性與內積參數的更復雜的內部邏輯進行比較。

密碼學與密碼經濟學

許多區塊鏈設計中出現的一個重要設計選擇是密碼學與密碼經濟學的選擇。通常這以在有效性證明和欺詐證明之間進行選擇的形式出現。

以太坊創始人Vitalik：若區塊鏈淪為富人的工具 整個行業將變得無趣:Vitalik近期在采訪中分享了自己對區塊鏈的看法，他說：“如果只有富人才能使用區塊鏈，那么整個行業就會變得很無趣。”另外，他還對PoW和PoS進行了對比，他認為前者很容易造成硬件中心化，而后者通過適當的獎懲機制將更具優勢。[2018/1/5]

ZK-SNARK是一種復雜的技術。雖然可以在一篇文章中解釋它們如何工作背后的基本思想，但實際上實現ZK-SNARK來驗證某些計算所涉及的復雜性是計算本身的許多倍。有效地實施ZK-SNARK涉及具有特殊目的優化的電路設計、使用不熟悉的編程語言以及許多其他挑戰。另一方面，欺詐證明本質上很簡單：如果有人提出挑戰，您只需直接在鏈上運行計算。為了提高效率，有時會添加二進制搜索方案，但即使這樣也不會增加太多復雜性。

但是，雖然ZK-SNARK很復雜，但它們的復雜性是封裝的復雜性。另一方面，欺詐證明的相對簡單的復雜性是系統性的。以下是欺詐證明引入的系統復雜性的一些示例：

他們需要謹慎的激勵工程來避免驗證者的困境。如果在達成共識的情況下完成，他們需要額外的交易類型來證明欺詐，以及推理如果許多參與者競爭同時提交欺詐證明會發生什么。它們依賴于同步網絡。它們允許審查攻擊被用來提交盜竊行為。基于欺詐證明的Rollup要求流動性提供者支持即時提款。由于這些原因，即使從復雜性的角度來看，基于ZK-SNARKs的純加密解決方案也可能長期更安全：ZK-SNARKs存在一些人必須考慮的更復雜的部分，但它們存在更少的每個人不得不考慮的懸而未決警告。

其他示例

工作量證明——低封裝復雜度，因為機制極其簡單易懂，但系統復雜度更高。哈希函數——高封裝復雜性，但非常易于理解的屬性，因此系統復雜性低。隨機洗牌算法——洗牌算法可能內部復雜但導致易于理解的強隨機性保證，或者內部更簡單但導致更弱且更難以分析的隨機性屬性。礦工可提取價值——一個強大到足以支持復雜交易的協議在內部可能相當簡單，但這些復雜的交易可能會對協議的激勵產生復雜的系統性影響，因為它有助于以非常不規則的方式提出區塊的激勵。Verkle樹——Verkle樹確實有一些封裝的復雜性，實際上比普通的Merkle哈希樹要復雜得多。然而，從系統上講，Verkle樹呈現出與密鑰值映射完全相同的相對簡潔的界面。主要的系統復雜性“泄漏”是攻擊者操縱樹以使特定值具有非常長的分支的可能性；但是對于Verkle樹和Merkle樹，這種風險是相同的。

我們如何進行權衡？

通常，封裝復雜度較低的選擇也是系統復雜度較低的選擇，因此有一個選擇顯然更簡單。但在其他時候，您必須在一種復雜性和另一種復雜性之間做出艱難的選擇。在這一點上應該清楚的是，如果將復雜性封裝起來，那么它的危險性就會降低。系統復雜性帶來的風險并不是規范有多長的簡單函數；與其他部分交互的一個小的10行規范比原本被視為黑匣子的一個100行函數增加了更多的復雜性。

然而，這種偏好封裝復雜性的方法存在局限性。軟件錯誤可能出現在任何一段代碼中，并且隨著它變得越來越大，錯誤的概率接近1。有時，當您需要以一種意想不到的新方式與子系統交互時，最初封裝的復雜性可能會變得系統化。

后者的一個例子是以太坊當前的兩級狀態樹，它具有一棵賬戶對象樹，其中每個賬戶對象又擁有自己的存儲樹。

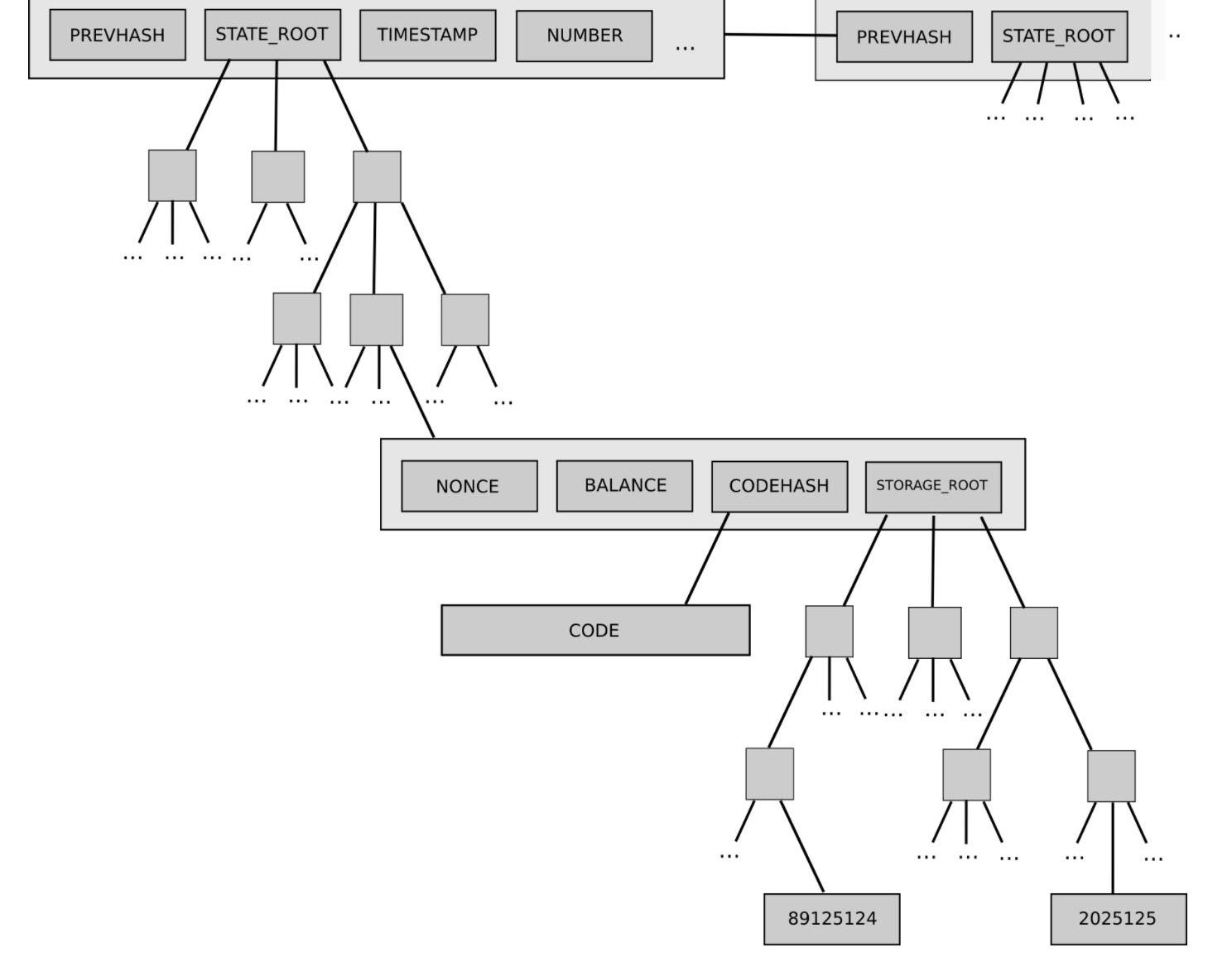
這種樹結構很復雜，但一開始復雜性似乎得到了很好的封裝：協議的其余部分與樹交互，作為您可以讀取和寫入的密鑰/值存儲，因此我們不必擔心關于樹的結構。

然而，后來證明復雜性產生了系統性影響：賬戶擁有任意大存儲樹的能力意味著無法可靠地期望狀態的特定部分有一個可預測的大小。這使得將狀態拆分為多個部分變得更加困難，從而使同步協議的設計和嘗試分配存儲過程變得復雜。為什么封裝的復雜性會變成系統性的？因為接口變了。修復？當前遷移到Verkle樹的提議還包括遷移到一種平衡良好的樹的單層設計。

最終，在任何給定情況下支持哪種類型的復雜性是一個沒有簡單答案的問題。我們能做的最好的事情就是保持適度支持封裝復雜性的態度，但不要過多，并在每個具體情況下行使我們的判斷力。有時，犧牲一點系統復雜性來大幅降低封裝的復雜性確實是最好的做法。在其他時候，您甚至可能會誤判什么是封裝的，什么不是。每種情況都不同。

Tags：VITITAVITATALIvite幣還能起來嗎CAKITAcurriculum-vitaeItalian Football Federation

MANA