COIN:零知識證明： Plookup算法介紹_looks幣投資機構

最近有空看了看Plookup的論文。針對對電路描述不友好的操作（比如bit操作），Plookup給出了新的思路和證明方式。給定某個操作的真值表示（lookup table），證明某個操作的輸入/輸出是在真值表中。這種方式，相對之前的bit計算約束方式，降低約束的個數，提高了電路效率。

Plookup的論文下載地址如下：

https://eprint.iacr.org/2020/315.pdf

基本思想

Plookup嘗試解決的問題是，給定兩個集合，證明某個集合的元素在另外一個集合中。給定兩個集合t和f，s是f排序后的結果。如果t中的元素最少在f中出現過一次。判別f中的元素是否包括在t中，只需要比較元素差的集合：

DoraHacks平臺開始支持基于零知識證明的隱私二次方資助:據官方消息，DoraHacks開發者激勵平臺HackerLink已經完成整合Dora Factory隱私投票模塊MACI，并開始支持基于零知識證明的二次方投票和二次方資助輪次。

MACI（最小化抗共謀基礎設施）是Dora Factory以太坊工廠的核心模塊之一，通過對投票進行加密以及對結果提供零知識證明，實現隱私投票，將鏈上和鏈下治理的投票過程轉化為非合作博弈，以達到抗共謀的目的。

DoraHacks對MACI代碼中的安全性和效率問題進行了系統性優化。ETH Denver 2022將于2月20日與DoraHacks共同推出第一個中等規模的MACI二次方資助輪次，超過2,000名開發者和10,000名參會者將通過DoraHacks平臺進行零知識二次方投票，這是MACI和鏈上隱私投票的第一次中等規模應用。[2022/1/28 9:19:46]

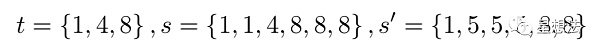
波卡聯合創始人：財政部很快將為零知識擴展和網絡基礎設施發展提供巨額資金:1月23日消息，波卡聯合創始人Robert Habermeier發推表示，Polkadot財政部可能很快就會為進一步發展零知識擴展和網絡基礎設施提供巨額資金。Exit-to-DAO作為一種商業模式將是2022年及以后的決定性變化。[2022/1/23 9:08:17]

舉個例子，t是{1，4，8}的集合，元素的差異集合為{3, 4}，分別是4-1，8-4。如果s只有t中的元素組成，并且每個元素最少出現一次，例如{1，1，4，8，8，8}，元素的差異集合也為{3，4}。如果s中的元素并不完全是t中的元素，那即使在元素差異集合一樣的情況下，也不能說明s中元素在t的集合中。例如s為{1，5，5，5，8，8}，元素的差異集合也為{3，4}，分別是8-5，5-1。

Filecoin：Filecoin網絡已成為最大的零知識證明網絡:Filecoin發表博客稱，目前Filecoin已成為最大的零知識證明（zk-SNARK）網絡。據官方數據顯示，目前Filecoin網絡每日會運行6至7百萬次零知識證明，每一個零知識證明中包含了超過1億個約束電路證明。目前Filecoin網絡的可信配置已支持最高128M大小的電路證明，單個證明最大已超過100M，而Zcash最高僅支持2M。此外，目前Filecoin實現了通過SnarkPack將10個零知識證明捆綁至單次證明中，并正在研究零知識證明聚合以實現將數千個零知識證明聚合至單次證明中。硬件支持方面，Filecoin將零知識證明中高度可并行化的部分交由GPU完成，將CPU和內存釋放出來進行較為復雜的計算，進一步提高了零知識證明的效率。[2021/7/14 0:51:01]

論文提出，可以引入一個隨機因子，將前后兩個元素相加的方法，確定兩個集合的依賴關系。

定義多項式

在基本思想的基礎上，論文在第三章定義了兩個多項式F和G：

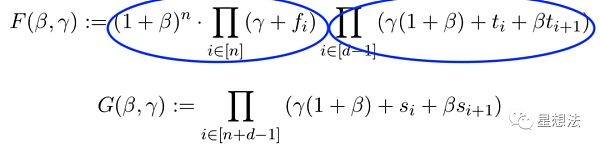
如果F和G相互對等，有且如下的條件成立：

f集合屬于t

s是(f，t)的并集，并且按照t中的元素排序

如果條件成立，可以推導出兩個多項式相等。F多項式可以看成是兩部分組成，分別是兩個連乘。后面的連乘可以看成是t中的元素連乘。前面的連乘，可以看成是f中元素的連乘。因為f中的元素屬于t，則f中的元素的連乘，可以想象成多個相同元素的連乘。反之，因為beta和gamma的隨機因子，也能從F和G對等條件推出滿足的兩個條件。具體的證明過程，可以查看論文的第三章。

在定義多項式的基礎上，問題可以轉化成兩個多項式相等。

Plookup協議

已知f和t，可以排序得到s。因為s由f和t合并而成，s可以由兩個函數h1和h2表示。關鍵在于第4步，定義了Z函數：

Z(g) = 1 - 初始為1

Z(x) 是兩種多項式表示的商

Z(g^(n+1)) = 1 - n+1元素的連乘，兩種多項式表達式相等

驗證者，除了查看Z函數外，額外還要查看h1/h2連續性。

論文進一步將協議推廣到更通用的情況，并給出了t中元素是連續情況下的優化協議。感興趣的小伙伴可以自行查看。

Plookup提出了一種明確輸入/輸出的情況下，如何證明某個函數的運算正確的協議。輸入輸出定義成lookup表，計算的輸入/結果只要在該lookup表中即表示運算正確。和Plonk采用同樣的思路，Plookup定義了問題的多項式表示，證明了Z函數的遞歸表示和邊界。

Tags：OKULOOKCOINFilecoinSokuSwaplooks幣投資機構coinw幣贏官方最新版下載Filecoin幣

幣贏